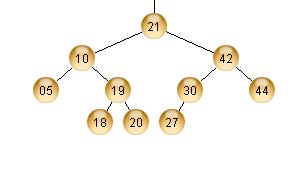
AVL-ominaisuus säilyy: Jokaisen solmun lapsien korkeudet eroavat toisistaan korkeintaan yhdellä. Erityisesti solmun 10 lapsien (5 ja 19) korkeudet ovat 0 ja 1; ja solmun 21 lapsien (10 ja 42) korkeudet ovat 2 ja 2.
return k1 jne.)
Mutta jos lisäykset ovat menneet niin pieleen, että puu ei ole enää edes hakupuu, voi käydä niin, ettei poistoja ole edes mahdollista tehdä oikein, kun "vasemman maksimi" tai "oikean minimi" ei ole oikealla paikallaan. Silloin ei poistostakaan saanut pistettä.
b)
Kierto sinänsä (linkkien siirtely) osattiin varsin hyvin. Tyypilliset
virheet olivat, että korkeuskenttiä ei lainkaan muistettu päivittää,
tai ei huomattu, että kierrossa alipuun juuri vaihtuu ja jotenkin pitäisi saada tämä tieto välitettyä alipuun vanhemmalle. Luentomateriaalissa tämä informointi hoidetaan niin, että kiertometodi palauttaa kutsujalleen viitteen alipuun uuteen juureen, ja kutsuja sijoittaa saamansa viitteen sinne, minne se kuuluu, ks. esimerkkivastaukset alempana.
(Muitakin tapoja on, esim. jos solmuille oletetaan "isäviitteet" lapsiviitteiden lisäksi, voi kiertometodi tietysti käydä suoraan muuttamassa isän lapsiviitteen oikeaksi... mutta sitten pitäisi huomioida sekin tilanne, että ollaan koko puun juuressa!)
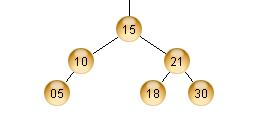
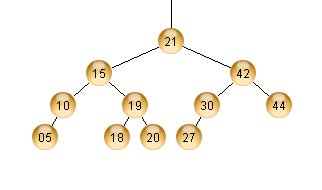
Kun 15 poistetaan "vasemman maksimi"-periaatteella, nousee siis 10 sen tilalle:

AVL-ominaisuus säilyy: Jokaisen solmun lapsien korkeudet eroavat toisistaan korkeintaan yhdellä. Erityisesti solmun 10 lapsien (5 ja 19) korkeudet ovat 0 ja 1; ja solmun 21 lapsien (10 ja 42) korkeudet ovat 2 ja 2.
Jos sensijaan 15 poistetaan "oikean minimi"-periaatteella, nousee 18 sen tilalle:
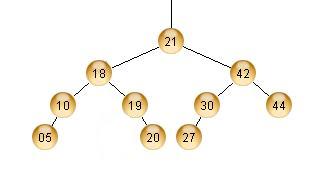
AVL-ominaisuus säilyy: Jokaisen solmun lapsien korkeudet eroavat toisistaan korkeintaan yhdellä. Erityisesti solmun 18 lapsien (10 ja 19) korkeudet ovat 1 ja 1.
Kuvat on tehty osoitteesta http://www.seanet.com/users/arsen/avltree.html löytyvällä AVL-appletilla.
b)
Selitys:
Yksöis- ja kaksoiskierto ovat paikallisia, vakioajassa O(1) tapahtuvia operaatioita, joilla AVL-ehto saatetaan uudestaan voimaan tietyn
"kiertosolmun" kohdalla, siten, että puu edelleen säilyy hakupuuna eli alipuiden sisällöt edelleen noudattavat järjestysrelaatiota.
Kierrot tapahtuvat alipuita sopivasti siirtelemällä.
Yksöiskiertoa käytetään, kun liikaa korkeutta on oikean lapsen oikeassa lapsessa (-> kierto vasemmalle) tai vasemman lapsen vasemmassa lapsessa (-> kierto oikealle).
Kaksoiskiertoa käytetään "siksak-tilanteissa": kun liikaa korkeutta on oikean lapsen vasemmassa lapsessa (-> kaksoiskierto vasemmalle) tai vasemman lapsen oikeassa lapsessa (-> kaksoiskierto oikealle).
(Vastaukselta ei vaadittu läheskään näin pitkää selitystä.)
Toteutus:
Kaksoiskierron voi tehdä kahdella yksöiskierrolla, jolloin tietysti
yksöiskiertojenkin toteutus on annettava (ks. yksinkertainen kierto ja kaksinkertainen kierto
luentomateriaalissa).
private static AVLSolmu kaksoisKiertoVasemmalle(AVLSolmu k3) {
k3.oikea = kiertoOikealle(k3.oikea);
return kiertoVasemmalle(k3);
}
private static AVLSolmu kiertoOikealle(AVLSolmu k2) {
AVLSolmu k1 = k2.vasen;
k2.vasen = k1.oikea;
k1.oikea = k2;
k2.korkeus = maksimi(korkeus(k2.vasen), korkeus(k2.oikea)) + 1;
k1.korkeus = maksimi(korkeus(k1.vasen), k2.korkeus) + 1;
return k1;
}
private static AVLSolmu kiertoVasemmalle(AVLSolmu k1) {
AVLSolmu k2 = k1.oikea;
k1.oikea = k2.vasen;
k2.vasen = k1;
k1.korkeus = maksimi(korkeus(k1.oikea), korkeus(k1.vasen)) + 1;
k2.korkeus = maksimi(korkeus(k2.oikea), k1.korkeus) + 1;
return k2;
}
private static int korkeus(AVLSolmu t) {
return (t == null) ? -1 : t.korkeus;
}
private static int maksimi(int eka, int toka) {
return (eka > toka) ? eka : toka;
}
Kaksoiskierron voi tehdä myös kokonaan yhdessä metodissa.