Y100 (matematiikka) - Tietokonelaskariosio, syksy 2006

Microsoft Excel -osio

Numeerisia menetelmiä ja tilastollisia perustoimintoja

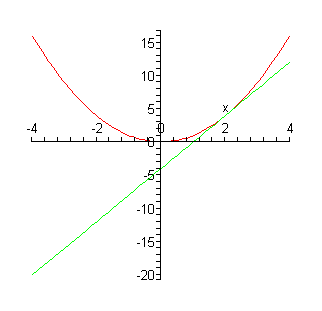
Excelin perusteet

Microsoft Excel on erinomaisesti numeerisiin operaatioihin sopiva ns. taulukkolaskentaohjelma. Se pystyy myös piirtämään kuvaajia numeroarvojen perusteella sekä lisäämään kuvaajiin tilastollisten operaatioiden graafisia kuvauksia (esim. regressiokäyriä).

Excel löytyy yliopiston mikroverkossa koneilta kansiosta Office. Mikäli Exceliä ei Office-kansiossa näy, on syytä etsiä sitä Installations-kansiosta ja yrittää asentaa.

Excelin avautuessa näkyviin tulee tyhjä työtila, taulukko, joka koostuu soluista. Solut järjestyvät pystysuunnassa sarakkeiksi ja vaakasuunnassa riveiksi. Jokaisella sarakkeella on kirjain ja jokaisella rivillä numero. Yksittäisten solujen nimet muodostetaan sarakkeen kirjaimesta ja rivin numerosta (esim. B7).

Soluihin voi kirjoittaa tekstiä, lukuja tai kaavoja. Mikäli soluun kirjoittaa ainoastaan numeroita, Excel tulkitsee solun sisällön luvuksi (huom. käytössämme olevassa suomenkielisessä Excelissä desimaalierottimena toimii pilkku). Kaavat taas on aloitettava yhtäsuuruusmerkillä (=), muuten Excel ei ymmärrä niitä.

Excel osaa suorittaa tavallisia aritmeettisia operaatioita kaavoissa. Esim. kirjoitetaan soluun "=3*(5+2^2)" ja painetaan ENTER. Soluun tulee luku 27, mutta solun kaava näkyy työtilan yläreunassa olevalla muokkausrivillä.

Kaavoja voi muokata klikkaamalla muokkausriviä tai kaksoisklikkaamalla solua. Muokkauksen jälkeen on aina painettava ENTERiä, muuten kaava rupeaa muuttumaan omia aikojaan, kun käyttäjä yrittää kirjoittaa muihin soluihin. Tämä johtuu siitä, että Excelissä kaavan osana voi olla myös solu.

Solu kaavan osana meritään solun nimellä, esim. "=B2+4" antaa tulokseksi solun B2 luvun ja nelosen summan. Kaavaa voidaan ajatella funktiona f(x)=x+4, jolloin kaavan sisältävään soluun tulostuu funktion arvo ja x:n paikalla olevaan soluun voi syöttää lähtöarvoja.

Mikäli annettu lähtöarvo ei kuulu määrittelyjoukkoon, Excel antaa kaavaruutuun tulokseksi virheilmoituksen. Esim. kirjoitetaan ruutuun B2 luku 0 ja ruutuun C2 kaava "=B1/B2" ja painetaan enter. Tällöin Excel vastaa "#DIV/0!", mikä tarkoittaa, että on yritetty jakaa nollalla, toisin sanoen funktio ei ole määritelty.

Excelissä solujen sisältöä voi kopioida "älykkäästi" toisiin soluihin viemällä hiiren osoitin solun oikeaan alanurkkaan, jolloin osoitin muuttuu mustaksi ristiksi, sitten tarttumalla solun kulmaan ja vetämällä haluttuun suuntaan. Tällöin Excel kopioi solun sisällön "älykkäästi" muokattuna niin pitkälle ja siihen suuntaan mihin vedetään. Älykkyys tarkoittaa, että kopioiduissa soluissa olevat kaavat eivät viittaa samaan ruutuun kuin alkuperäisen solun kaavat, vaan kopioidusta solusta samalla etäisyydellä kuin alkuperäisestä olevaan soluun. Esim. Jos kopioit kaavan "=B2+C2" sisältävää solua alaspäin, seuraavaan soluun tulee kaava "=B3+C3", sitä seuraavaan "=B4+C4" ja niin edelleen.

Toinen Excelin kopiointiominaisuuden sovellus on aritmeettisen sarjan jatkaminen. Jos esim. kirjoitat päällekkäisiin soluihin luvut 1, 2 ja 3, valitset ensin normaaliosoittimella (valkoinen risti) vetämällä nuo solut ja kopioit valittua aluetta alaspäin oikeasta alanurkasta mustalla ristiosoittimella vetämällä, tulee seuraaviin ruutuihin luvut 4, 5, 6 jne. Samaten voit kopioida sarjaa 3, 6, 9, jolloin Excel jatkaa sarjaa: 12, 15, 18 jne. Muista, että "älykäs kopiointi" toimii yhtä lailla alas, ylös, vasemmalle ja oikealle!

Harjoitus 1. Ilmaise funktiot f(x)=x^3+2x^2+3 ja g(x)=(4x^2+1)/(-x^2+x) Excelissä kaavoina, joissa x:n tilalle tulee jokin ruutu. Kokeile funktion arvoja eri lähtöarvoilla sijoittamalla lähtöarvo ko. ruutuun. Tarkistus: ensimmäisen funktiona arvo lähtöarvolla 2 pitäisi olla 19, toisen 2,833333...

Harjoitus 2. Muodosta sarja 1, 3, 5, 7 ... päällekkäisiin soluihin. Muodosta näiden solujen viereen sarja kaavoja, joka antaa tulokseksi viereisen solun arvon kerrottuna kahdella ja vähennettynä sitten yhdellä.

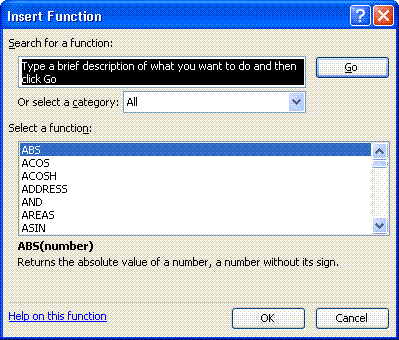
Datan käsittelyyn Excelissä on tarjolla lukuisia valmiiksi tehtyjä toimintoja, funktioita (tämä ei ole aivan sama kuin matematiikan käsite "funktio"). Käymme tässä läpi muutamien yleisten Excelin funktioiden käytön ja tehtävät. Funktion voi lisätä tyhjään soluun valitsemalla Insert-valikosta komennon "Function...", jolloin näkyviin tulee funktionvalintaikkuna. Kohdasta "Or select a category:" voi hiirellä valita, minkätyyppiset funktiot alla olevassa listassa näkyvät; kaikki funktiot saa näkyviin valitsemalla "All". Funktion voi valita listasta ja painaa sitten OK tai "Help on this function" (ikkunan vasemmassa alakulmassa), jolloin Excel antaa tietoja valitsemasi funktion käytöstä.

Funktion voi lisätä Exceliin myös kuten minkä tahansa muunkin kaavan: kirjoittamalla soluun "=FUNKTIO(arvot)", missä FUNKTIO on valitsemasi funktion nimi. Funktion jälkeen tulee suluissa yksi tai useampia lähtöarvoja, joiden perusteella Excel sitten laskee soluun jonkin arvon. Lähtöarvot erotetaan toisistaan puolipisteellä. (Jos desimaalierottimena on piste, puolipisteen tilalla käytetään pilkkua.)

Tyypillisiä funktioita ovat esim. itseisarvofunktio ABS, summafunktio SUM, potenssi- ja neliöjuurifunktiot POWER ja SQRT, trigonometriset funktiot SIN, COS ja TAN, eksponenttifunktio EXP, logaritmifunktiot LN, LOG ja LOG10, muuntofunktiot DEGREES, RADIANS, ROUND ja INT, satunnaisfunktio RAND, loogiset funktiot AND, OR ja NOT, ehtofunktio IF, ja soluja laskeva COUNT. Seuraavaksi selitän näiden toimintaa esimerkein.

Itseisarvo, neliöjuuri ja trigonometriset funktiot ovat aika selkeitä: lasketaan suluissa olevan luvun ko. funktio.

kaava	vastaus
=ABS(-2)	2
=SQRT(100)	10
=SIN(2)	0,909297427
=COS(2)	-0,416146837
=TAN(2)	-2,185039863

Huomaa, että trigonometriset funktiot olettavat syötetyn arvon olevan radiaaneja!

Luvun tilalle voi Excel-kaavassa aina syöttää myös solun nimen, siten esim. "=ABS(E3)" laskee ruudussa E3 sijaitsevan luvun itseisarvon.

Potenssifunktio POWER on sama kuin potenssiin korotus ^-merkillä. POWER saa kaksi argumenttia, ensin korotettavan luvun ja sitten eksponentin. Huomaa, että erillistä juurifunktiota korkeammille juurille ei ole, vaan niiden arvot pitää laskea korottamalla vastaavaan murtopotenssiin!

SUM-funktio laskee annettujen argumenttien summan. Tavallisesti tätä funktiota käytetään jonkin taulukkoalueen kaikkien lukujen summaamiseen, jolloin alueen vasemman yläkulman solu ja oikean alakulman solu ilmoitetaan yhtenä argumenttina kaksoispisteellä erotettuina.

kaava	vastaus
=POWER(3;3)	27
=SUM(5;6;7;8;9)	35
=SUM(A1:C8)	solujen A1-A8, B1-B8 ja C1-C8 sisältöjen summa
=SUM(A1:A8;C1:C8)	sama kuin yllä lukuunottamatta soluja B1-B8

EXP-funktio palauttaa luvun eksponenttifunktion, ts. e potenssiin annettu luku, likiarvon (kuten Maplessakin jos laksetaan desimaaliluvuilla). Luvun e likiarvon saa luonnollisesti kirjoittamalla =EXP(1). LN ja LOG10 taas ovat e- ja 10-kantaiset logaritmit, ja LOG on yleinen logaritmi, jonka jälkeen sulkuihin kirjoitetaan ensin lähtöarvo, sitten logaritmin kantaluku.

kaava	vastaus
=EXP(1)	2,718281828
=LN(2,718281828)	1
=LOG10(100)	2
=LOG(8;2)	3

Muuntofunktiot DEGREES ja RADIANS muuntavat radiaaneja asteiksi ja päinvastoin. Saman asian ajaa toki kertominen tai jakaminen pii*180:llä (johon tulemme tämän osan lopussa). ROUND pyöristää ensimmäiseksi argumentiksi kirjoitettavan luvun niin moneen desimaaliin kuin ilmaistaan toisessa argumentissa ja INT palauttaa luvun kokonaislukuosan. RAND antaa satunnaisluvun 0:n ja 1:n väliltä, ja se arvotaan uudelleen mm. joka kerta kun tiedosto avataan. INT-funktio voi olla kätevä satunnaisten kokonaislukujen saamiseen: esim. "=INT(RAND()*6)+1" vastaa tavallisen nopan heittämistä. (Ilman "+1":tä lopussa saataisiin satunnaisia arvoja 0:sta 5:een.) RANDin jälkeen kirjoitetaan sulut, mutta niiden sisälle ei tule mitään.

kaava	vastaus
=DEGREES(2)	114,591559
=RADIANS(180)	3,141592654
=ROUND(2,7;0)	3
=INT(2,7)	2
=INT(RAND())	joko 0 tai 1

Loogisilla funktioilla sekä ehtofunktiolla voidaan rakentaa mutkikkaampia laskurakenteita, joiden toiminta riippuu esim. määrättyjen solujen sisällöstä. IF-funktio saa kolme argumenttia, joista ensimmäinen on väite, esimerkiksi "C3>0". Jos väite on tosi (tässä tapauksessa solussa C3 on positiivinen luku), solun, jossa IF-lause on, arvoksi tulee toinen argumentti. Jos väite ei ole tosi, arvoksi tulee kolmas.

ANDin, ORin ja NOTin toiminta on hieman samantapaista: AND-funktiolle annetaan kaksi tai useampia väitteitä. Jos kaikki väitteet ovat tosia, AND-funktio saa arvon TRUE, muutoin FALSE. OR-funktiossa riittää, että yksi väitteistä on tosi ja NOT-funktio antaa päinvastaisen totuusarvon kuin sille annettu väittämä. Tyypillistä loogisten funktioiden käyttöä on niiden sijoittaminen IF-funktion sisään.

kaava	vastaus
=IF(A3+A4=3;1;0)	Jos A3+A4=3 niin 1, muutoin 0
=AND(1+1=2;2+2=4)	TRUE
=OR(3=0;1*1=-1)	FALSE
=NOT(1+1=2)	FALSE
=IF(AND(A3+A4=3;A5+A6=3);A7;A8)	Jos molemmat yhtälöt ovat tosia, ruudun A7 sisältö, muutoin ruudun A8.

COUNT laskee annetulla alueella ne solut, joissa on numeroarvo. Myös nollat lasketaan. Tämä voi olla kätevä esim. aineiston kokoa edustavan lukuna.

	A	B
1	114,591559	=COUNT(A1:A5)
2
3	3
4
5	Böö

tuloksen pitäisi olla 2.

Huom! Piin likiarvon Excel ilmoittaa funktion PI() avulla. Tämäkään funktio ei käytä argumenttia. Niinpä esim. DEGREES-toiminto voidaan suorittaa myös vaikkapa näin: =DEGREES(x) ajaa saman asian kuin =x*180/PI(). (=RADIANS(x) on sitten sama kuin =x/180*PI()!)

Opettelemme laskemisen lisäksi piirtämään Excelillä kuvaajia annetusta datasta. Tätä ominaisuutta tarvitsemme mm. tilastollisissa menetelmissä, joita opiskellaan kurssin loppupuolella. Samalla hahmottelemme funktioiden kuvaajia arvopisteiden avulla. Tämä on periaatteessa sama menetelmä, jolla kuvaajia muodostetaan käsin: lasketaan funktion arvoja erilaisilla lähtöarvoilla ja piirretään arvopisteiden avulla likimääräinen kuvaaja.

Piirretään ensin funktion f(x)=(x^3)/2 (eli 1/2(x^3)) kuvaaja. Tätä varten lasketaan funktion arvoja sillä alueella, jolla kuvaajaa halutaan tutkia. Valitsemme nyt alueeksi välin [-6, 6]. Emme kuitenkaan voi laskea funktion kaikkia arvoja ko. välillä - niitähän on äärettömän paljon. Mikäli arvoja lasketaan riittävän tiheästi, saadaan kuitenkin funktion kuvajalle riittävän tarkka approksimaatio (tarkoituksesta riippuen). Kokeillaan arvojen laskemista 0,5:n välein, siis pisteissä -6; -5,5; -5; -4,5... ja sijoitetaan sitten pisteet kuvaajaan.

Aluksi tarvitsemme Excel-taulukon, jossa näkyvät funktion lähtöarvot ja arvot vierekkäisissä sarakkeissa. Funktion arvoja ei tarvitse laskea käsin, vaan ne saadaan Excelillä vaikkapa seuraavasti: Sijoitetaan ensin numerot -6 ja -5,5 valituista lähtöarvoista A-sarakkeeseen siten, että ruudussa A1 on luku -6 ja ruudussa A2 luku -5,5. Loput luvut sarakkeeseen saadaan maalaamalla eli valitsemalla aluksi ruudut A1 ja A2 vetämällä hiiren valkea ristiosoitin ruutujen päältä vasen nappi pohjassa ja jatkamalla sitten sarjaa vetämällä valitun alueen oikeasta alanurkasta alaspäin mustalla ristiosoittimella riittävän pitkälle.

Kirjoitetaan nyt soluun B1 kaava, joka antaa funktion arvon viereisessä solussa olevalla lähtöarvolla eli "=(A1^3)/2". Muista painaa ENTER kirjoitettuasi kaavan. Jos painat hiirellä jotain solua kaavaa kirjoittaessasi, Excel kirjoittaa automaattisesti tämän solun nimen siihen kohtaan kavaa, jossa olet! Tämä on syytä ottaa huomioon. Solun nimen saat kaavaan kuitenkin myös käsin kirjoittamalla.

Kaava on muuten sama kuin funktion lauseke, mutta alkuun ei tarvita f(x):ää (eli funktion nimeä) ja muuttujan paikalle kirjoitetaan ruutu, jossa muuttuja sijaitsee. Painettuasi ENTER ruudussa B1 pitäisi lukea funktion arvo -108. Kaava on kuitenkin edelleen ruudussa, minkä näet solun valitessasi ruudun yläosassa työkalurivien alla sijaitsevalla funktiorivillä (symboli "fx") tai kaksoisklikkaamalla solua.

Kun kaava on valmis, voit tarttua kaavasolua niinikään oikeasta alakulmasta mustalla ristiosoittimella ja vetää alaspäin. Tämä täyttää alkuarvojen viereiseen sarakkeeseen funktion kaavat (ja niiden tuloksina arvot). Tutkimalla kopioituja kaavoja B-sarakkeessa huomaat, että kopioidessaan kaavaa alaspäin Excel on myös sijoittanut joka kaavaan arvoruuduksi vastaavan viereisen sarakkeen ruudun; B2:ssa arvoruutu on siis A2, B3:ssa A3, B4:ssä A4 jne. Jos jossain sovelluksessa et halua Excelin muuttavan kaavaa vetämällä kopioitaessa vastaamaan uuden ruudun sijaintia, on solun nimi ilmaistava kaavassa muodossa "$A$1", missä "A":n paikalle tulee solun kirjain ja ykkösen paikalle numero. Dollarimerkki ($) kiinnittää sen koordinaatin, jonka edessä se on solun nimessä siten, että siirrettäessä tai kopioitaessa ko. koordinaatti ei muutu kaavan uutta sijaintia vastaavaksi.

kahden ensimmäisen sarakkeen pitäisi nyt näyttää tältä:

Jos olisimme hahmottelemassa kuvaajaa käsin, laskisimme vähemmän arvopisteitä ja pyrkisimme löytämään funktion kulun kannalta olennaisia pisteitä (esim. jos funktio saa hyvin lähellä toisiaan olevia arvoja, kannattaa kokeilla kauempana olevilla lähtöarvoilla). Excelillä voimme kuitenkin laskea vaivattomasti hyvinkin paljon pisteitä. Jotain rajaa kannattaa silti tässäkin tapauksessa pitää: Hyvin suuren aineiston piirtäminen kuvaajaan on joillakin laitteistoilla hidasta ja sitäpaitsi taulukkoa voi joutua selailemaan hankalasti ylös ja alas.

Piirrämme kuvaajan Excelin graafityökalulla, joka löytyy päätyökalurivin loppuvaiheilta. Valitse ensin hiirellä koko luomasi taulukko ja paina sitten graafityökalua:

Esiin tulee ikkuna "Chart Wizard - Step 1 of 4 - Chat Type", jossa on valittavana kaksi välilehteä. Pysymme "Standard Types" -välilehdessä ja valitsemme vasemmanpuoleisesta valikosta vaihtoehdon "XY (Scatter)". Tämä valinta tuottaa pistediagrammin, jossa vasen sarake tulkitaan automaattisesti x-akselin arvoiksi ja oikea sarake y-akselin arvoiksi. Pisteet voi myös yhdistää viivoilla, mikä tehdään valitsemalla oikeanpuoleisesta "kuvavalikosta" keskimmäisen rivin vasemmanpuoleinen tyyppi:

Sitten siirrytään kaavion luonnin seuraavaan vaiheeseen painamalla hiirellä "Next >" -nappia. Huomaa, että muita kaaviotyyppejä käyttäessäsi Excel käyttää kullekin kaaviotyypille sisäänrakennettuja oletuksia. Esim. nyt tehtävän kaavion pystyisi toteuttamaan myös viivadiagrammitoiminnolla, mutta valintoja pitäisi tehdä kaaviota luodessa enemmän - Excel olettaa viivadiagrammia tehdessään, että x-akselilla ei ole mitään erityisiä arvoja, vaan peräkkäiset ruudut tulevat "peräkkäisiin kohtiin" x-akselilla. Tämän pystyy muuttamaan, mutta se vaatii hieman lisäpuuhaa. Samaten muita diagrammityyppejä, esim. kakkudiagrammia tai ensimmäisen ikkunan toisesta välilehdestä löytyviä "mukautettuja tyylejä" koskevat omat alkuoletuksensa, joita sitten ehkä joutuu kiertämään, mikäli aineisto ei ole juuri ko. oletuksille soveltuva. Kannattaa kokeilla eri kaaviotyyppejä ja valintoja eri vaiheissa kaavion luontia ja miettiä sitten, millä logiikalla Excel minkäkinlaisen kaavion annetuista arvoista loi!

Seuraavan vaiheen voimme sivuuttaa painamalla uudestaan "Next >" -nappia. Tässä vaiheessa oltaisiin korjattu Excelin virheelliset tulkinnat taulukon arvojen merkityksistä, jos oltaisiin valittu viivadiagrammitoiminto. Voit tässäkin vaiheessa kokeilla, miten eri valinnat kaavioon vaikuttavat; apuna on ikkunassa näkyvä tulevan kaavion esikatselu.

Seuraavassa vaiheessa ikkunan otsikossa pitäisi lukea "step 3 of 4". Kirjoitamme (näkyvillä olevaan) "Titles"-välilehteen kaaviolle otsikon ja akseleille nimet. Kaavion otsikoksi voi laittaa vaikkapa "f(x)=(x^3)/2". Tämä kirjoitetaan kohtaan "Chart title:". Kahteen alempaan ruutuun kirjoitamme akselien nimet: x-akselille nimen "x" ja y-akselille "f(x)". Sitten valitsemme välilehden "Legend" ja otamme ruksin pois ruudusta "Show legend". Tällöin oikealla näkyvästä kaavion esikatselusta häviää funktion arvojen selite. Emme nyt tarvitse selitettä, koska meillä on vain yksi tutkittava arvosarja, jolla ei ole sen kummempaa nimeä. Selitettä voisi käyttää esim. useamman funktion tapauksessa.

Valitsemme vielä kerran "Next >". Prosessin viimeinen vaihe kysyy, upotetaanko kaavio muokattavaan taulukkosivuun vai tehdäänkö siitä oma sivunsa. Kätevyyssyistä valitsemme upotetun kaavion ("As object in:") ja painamme "Finish". Esiin tulee kaavio, jonka päällä on kaavion muokkaustyökalu:

Kaaviota voi siirtää vetämällä sen valkoisesta alueesta ja sen kokoa voi muokata tarttumalla ja vetämällä mustista neliöistä sen reunoilla. Näin hahmottelimme arvopisteiden avulla kysytyn funktion kuvaajan. Jos kuvaajasta ei tule jollakin funktiolla valaiseva, kannattaa kokeilla funktion arvojen laskemista tiheämmässä tai harvemmassa olevilla pisteillä eri puolilla määrittelyjoukkoa. Graafi päivittyy sitä mukaa kun sen arvoalue taulukossa muuttuu! Kokeile esim. mitä tapahtuu, jos muutat jonkin lähtöarvoista toiseksi, esim. -10:ksi.

Muunkinlainen kokeilu ja graafityökalun eri valintojen tutkiminen on tämän tehtävän yhteydessä suotavaa!

Harjoitus 3. Tee kuvaaja funktiosta f(x)=1/(x^2). Kuinka selkeä kuvaajasta tuli? Mitä kone piirtää funktion arvoksi pisteeseen 0, jos sitä yritetään piirtää? Onko tämä oikein? Mitä funktiolle tapahtuu tässä pisteessä?

Harjoitus 4. Yritä saada samaan kuvaan kuvaaja funktioista f(x)=x^2 ja g(x)=2. Miten tämä voisi onnistua? Miten saat kuvaajaan haluamiasi (x, y)-pisteitä, joita ei määrittele erityisesti mikään funktio?

Seuraavaksi tutustumme muutamaan numeeriseen menetelmään. Nämä menetelmät on valittu pikemmin helposti ymmärrettävinä ja periaatetta opettavina esimerkkeinä, niin Excelin käytön kuin matematiikankin kannalta katsottuna, kuin käytännössä yleisimpinä menetelminä; käytännössä esiintyvät numeeriset menetelmät ovat usein liian monimutkaisia tässä selitettäviksi ja menetelmät vaihtelevat sovellusalueen mukaan. Numeeristen menetelmien periaatteet ovat kuitenkin usein esimerkkiemme kaltaisia.

Funktioiden ja yhtälöiden yhteydessä usein esiin tuleva tehtävä on nollakohtien löytäminen. Aina se ei ole kuitenkaan analyyttisin menetelmin mahdollista tai ainakaan helppoa. Esimerkiksi neljännen asteen polynomin yleinen ratkaisukaava on niin pitkä, ettei sitä juurikaan käytetä, ja viidennestä asteesta ylöspäin yleisiä ratkaisukaavoja ei ole olemassa.

Ensimmäinen menetelmä, johon tutustumme on ns. puolitus- eli haarukointimenetelmä funktion nollakohtien löytämiseksi. Menetelmä on logiikaltaan yksinkertainen ja selkeä. Nollakohtien ratkaisuun on helppo käyttää numeerisia menetelmiä Excelissä, mikäli yhtälöitä ratkaisevaa ohjelmaa, esim. Maplea ei ole käytössä.

Puolitusmenetelmän käyttöön vaaditaan eräitä esitietoja funktiosta, ja sen avulla voidaan etsiä vain yhtä nollakohtaa kerrallaan. Ensinnäkin funktion pitää olla määritelty välillä, jolla menetelmää käytetään, ja lisäksi sen on oltava jatkuva kyseisellä välillä. Nollakohtia löytyy vain, jos funktio vaihtaa merkkiä tutkittavalla välillä. Itse asiassa puolitusmenetelmässä funktion on oltava eri merkkinen välin alussa ja lopussa. Tällöinkin väliltä saattaa löytyä useita nollakohtia, mutta menetelmällä niitä löytyy vain yksi. Parasta on valita väli, jolta voimme olettaa löytävämme yhden nollakohdan, mikäli mahdollista.

Käytämme esimerkkinä puolitusmenetelmää funktion f(x)=x^3-2x erään nollakohdan etsimiseen. Ensin valitsemme välin, jolta nollakohtaa etsitään. Tämä tehdään arvaamalla. Jos käytettävissä tai tehtävissä on luonnos kuvaajasta, sen avulla voidaan muodostaa varsin hyväkin arvaus.

(kuva funktiosta)

Etsimme nyt nollakohtaa funktiosta välillä [1, 2]. Tässä tapauksessa näemme kuvaajasta, että nollakohta on jossakin tuolla välillä. Funktio on tällä alueella kasvava, joten täyttäessään ehdot, joilla menetelmää voi käyttää se saa negatiivisen arvon välin alkupisteessä ja positiivisen arvon loppupisteessä. Nyt puolitusmenetelmä toimii graafisesti näin:

Funktion arvoa tutkitaan valitun välin puolimatkassa. Mikäli ei käy niin hyvin, että funktion nollakohta on juuri tässä pisteessä, valitaan tarkasteltavaksi uusi, lyhyempi väli. Jos funktion arvo on puolituspisteessä positiivinen (kuten esimerkissä), siirrytään tarkastelemaan puolivälin alapuolista väliä (alkuperäisen välin alkupisteessähän funktio oli negatiivinen, joten nollakohdan pitää löytyä tältä väliltä) eli väliä [1, 1,5]. Jos funktion arvo puolituspisteessä tas olisi positiivinen, valittaisiin seuraavaksi tarkasteluväliksi [1,5, 2]. Huomaa, että jos funktio olisi ollut alkuperäisen välin alussa positiivinen ja lopussa negatiivinen, valinta tehtäisiin päinvastoin!

Seuraavaksi puolitetaan saatu uusi, lyhyempi väli ja lasketaan taas funktion arvo puolituskohdassa. Kuvassamme funktio saa tässä kohdassa jos hyvin lähellä nollaa olevan arvon. Toistetaan sama menettely kuin edellisessä kohdassa: jos funktion arvo on uudessa, lyhyemmän välin puolivälissä positiivinen, valitaan seuraavaksi tarkasteluväliksi tämän välin alempi puolisko [1, 1,25], muussa tapauksessa ylempi puolisko [1,25, 1,5]. (Huomaa taas, että meneteltäisiin päinvastoin, jos alkuperäisen välin päissä funktio olisi saanut erimerkkiset arvot kuin nyt!)

Tätä menetelmää toistamalla saadaan yhä lyhyempiä ja lyhyempiä valejä, joiden sisään funktion eräs nollakohta jää. Toisaalta välin puolimatka tarjoaa joka askeleella yhä tarkemman arvauksen nollakohdaksi. Excelissä puolitusmenetelmä voidaan toteuttaa vaikkapa näin:

Ensin kirjoitetaan funktio muistiin, esim. soluun A1. Sitten tehdään neljä saraketta: "välin alkupiste", "välin loppupiste", "puoliväli" ja "f(puoliväli)" eli funktion arvo puolivälissä. Huomaa, että mikäli teksti ei mahdu haluamaasi soluun, voit muuttaa sarakkeen kokoa vetämällä sarakkeen koordinaattiruutujen (harmaat ruudut, joissa on sarakkeen nimi) välistä mustalla kaksoisnuoliosoittimella. Tässä esimerkissä sarakkeiden nimet ovat ruuduissa C1-F1.

Aluksi kirjoitamme ruutuihin C2 ja D2 alkuperäisen välin alku- ja loppupisteet (siis tässä tapauksessa luvut 1 ja 2). Ruutuun E2 kirjoitamme näiden pisteiden puolivälin kaavan "=(C2+D2)/2". (Älä siis kirjoita lainausmerkkejä!) Kun kaava on valmis, ja painat ENTER, ruutuun pitäisi tulla laskun tulos, tässä tapauksessa 1,5. Sitten tarvitsemme funktion arvon puolivälipisteessä. Kirjoitamme ruutuun F2 kaavan, joka vastaa funktion arvon laskemista äsken lasketussa pisteessä: "=E2^2-2*E2". Tämän kaavan pitäisi antaa tulos 0,375. Nyt kaavion pitäisi näyttää jotakuinkin tältä:

Ruutuihin C3 ja D3 tarvitaan nyt uuden välin alku- ja loppupisteet. Tähän käytetään Exceliin sisäänrakennettua ehtolausetoimintoa. Uuden välin alkupistehän on tässä tapauksessa edellisen välin puoliväli, jos f(puoliväli) on negatiivinen (eli nollaa pienempi), muuten taas edellisen välin alkupiste. Excelin ehtolause on muotoa "=IF(testi; arvo jos testi onnistuu; arvo jos testi ei onnistu)". Tässä tapauksessa kirjoitamme ruutuun C3 siis "=IF(F2<0; E2; C2)". Näin Excel valitsee uuden välin alkupisteeksi edellisen puolivälin, jos arvo siinä on negatiivinen, muutoin edellisen välin alun. Jos alun perin olisimme valinneet välin, jolla funktion arvo on alussa positiivinen ja lopussa negatiivinen (tämän voi tarkistaa laskemalla), kaava olisi muuten samanlainen, mutta "<"-merkin tilalla olisi ">". Tämä johtuu siitä, että jouduttaisiin valitsemaan uusi väli juuri päinvastoin. Tätä voit tutkia vaikkapa piirtämällä itse kuvaajan päinvastaisesta tapauksesta.

Ruutuun D3 tarvitaan uuden välin loppupiste. Voidaan käyttää samaa kaavaa kuin edellisessä ruudussa sillä erotuksella, että tulokseksi pitää saada joko edellisen välin loppupiste tai puoliväli. Kaavaksi tulee siis "=IF(F2<0; D2; E2)". Tässäkin kaavassa olisi ">"-merkki "<"-merkin tilalla, jos alkuperäisen välin päätepisteiden merkit olisivat olleet toisin päin. Näiden kaavojen sijoittamisen jälkeen kaavion pitäisi näyttää tältä:

Nyt olemme kirjoittaneet kaikki tarpeelliset kaavat. Kone pitäisi vielä saada suorittamaan samat toimenpiteet uuden välin rajojen avulla. Tämä onnistuu Excelin kaavojen älykkäällä kopiointiominaisuudella. Valitaan siis ruudut C3 ja D3, tartutaan oikean alakulman mustasta neliöstä ja vedetään alaspäin. Kone täyttää taulukkoa kaavoja kopioimalla (siten, että seuraavalla rivillä kaavat viittaavat aina riviä alempiin lähtösoluihin). Aluksi tulevissa arvoissa ei ole järkeä. Siksi pitää kopioida myös solujen E2 ja F2 kaavoja samalla tavalla alaspäin. Taulukosta tulee nyt jotenkin tämän näköinen:

Nähdään, että välien puolivälit lähestyvät funktion nollakohtaa, sillä funktion arvot lähenevät nollaa. Mitä pidemmälle kaavoja kopioidaan, sitä tarkemmaksi arvio tulee. Mikäli et saa desimaaleja näkymään haluamallasi tavalla, valitse koko taulukko ja paina sen päällä hiiren oikeaa nappia. Valitse esiintulevasta valikosta "Format Cells..." ja muuta siellä numeroiden esitystapaa. (tähän tulee vielä tarkempi kuvaus, minulla on nyt käytössäni OpenOffice, joka saattaa tuossa poiketa hieman Excelistä)

Puolitusmenetelmällä saadaan esim. kysytylle funktion nollakohdalle arvo 1,414, jos sitä kysyttäisiin kolmen desimaalin tarkkuudella. Puolitusmenetelmä on numeerisista nollakohdanetsintämenetelmistä ymmärrettävin, mutta myös yksi tehottomimpia: tulos tarkentuu melko hitaasti. Seuraavaksi esittelemme parannetun ja tehokkaamman Newtonin menetelmän. Puolitusmenetelmän ymmärtäminen on kuitenkin hyvä johdatus numeeristen menetelmien maailmaan.

Harjoitus 5. Etsi samalla menetelmällä saman funktion toinen nollakohta väliltä [-2, -1]. Pohdi, mitä joudut tekemään merkinnöille ehtolausekkeissa ja miksi. Hahmottele sitten Excelillä sinifunktion kuvaaja ja etsi puolitusmenetelmällä sen nollakohtia väleiltä [2, 5] ja [1, 2]. Löytyikö nollakohtia? Mistä tiedät tämän? Mitä tapahtui jälkimmäisellä välillä?

Tehokkaampi menetelmä nollakohtien etsimiseen on ns. Newtonin menetelmä, joka perustuu funktion sivuajien eli tangenttien ominaisuuksiin. (Älä sekoita tätä tangenttifunktioon, vaikka määritelmien välillä onkin yhteys!) Graafisesti ottaen menetelmässä piirretään funktiolle sivuaja johonkin pisteeseen ja muodostetaan nollakohta-arvaus sen avulla. Arvaukseksi tulee sivuajan nollakohta.

Sitten piirretään uusi sivuaja funktiolle saadussa arvauskohdassa, ja sen nollakohdasta tulee uusi arvaus. Esimerkkikuvassamme tämä päätyy jo hyvin lähelle funktion todellista nollakohtaa.

Menettelyä toistetaan kuten puolitusmenetelmässäkin. Erona on se, että saatu arvaus lähestyy funktion nollakohtaa hyvin paljon nopeammin. Karkeana arviona voidaan esittää, että oikeiden desimaalien määrä arvauksessa yleensä suurin piirtein kaksinkertaistuu joka askeleella.

Newtonin menetelmän heikkous on, että se ei toimi aina, milloin puolitusmenetelmä toimii. Toisaalta kaikkia puolitusmenetelmän esitietoja ei tarvita (esim. ei ole mitään tarkasteluväliä, jonka eri päissä funktion pitäisi saada erimerkkiset arvot). Mielivaltaisella reaaliarvoisella funktiolla ei tietenkään aina edes ole nollakohtia, emmekä nyt käy läpi ehtoja, joilla Newtonin menetelmä toimii. Meille riittää seuraava tieto: jos Newtonin menetelmän antamat arvaukset lähestyvät jotain pistettä, piste on tutkittavan funktion eräs nollakohta. Toisia nollakohtia voi etsiä muuttamalla menetelmän lähtöpistettä. Hyviä lähtöpisteitä voi löytää funktion kuvaajaa hahmottelemalla.

Käyttääksemme Newtonin menetelmää numeerisesti meidän on pystyttävä muodostamaan funktiolle sivuajafunktio jossain pisteessä. Tämä tehdään funktion derivaatan avulla.

Derivaatan arvo tietyssä pisteessä kuvaa funktion jyrkkyyttä ko. pisteessä. Itse asiassa derivaatta on nimenomaan pisteeseen piirretyn sivuajan kulmakerroin. Tämä tarkoittaa sitä, että sivuajafunktion yhtälö on muotoa s(x)=kx+a, missä k on funktion f derivaatta ja a jokin vakio. Pisteessä x0 sivuaja s_x0 on siis s_x0(x)=f'(x0)x+a. Meidän pitää vielä ratkaista a.

Jos a olisi 0, s_x0:n kuvaaja kulkisi origon kautta. Siirrämme sitä ensin y-akselia ja sitten x-akselia pitkin, niin että saamme lopulta tulokseksi halutun sivuajan. Siirretään kuvaaja ensin kulkemaan arvolla x=0 siltä korkeudelta, millä sen pitäisi kohdata alkuperäinen funktio eli siirretään sitä y-akselia pitkin. Tämä tapahtuu lisäämällä a:han funktion arvo x0:ssa.

Nyt meillä on suora s_x0(x)=f'(x0)x+f(x0), siis sivuajan suuntainen suora, jossa a:na on funktion arvo sivuamispisteessä. Pitäisi vielä siirtää suoraa x-suunnassa siten, että se saisi pisteessä x0 sen arvon, jonka se nyt saa nollassa. Korvataan nyt suoran kaavassa esiintyvä x lausekkeella (x-x0), joka saa arvon 0, kun x=x0. Tällöin kuvaaja pysyy muuten samana, mutta siirtyy x0:n verran, koska se saa samat arvot kuin edellinen versio kohdissa, jotka ovat x0:n päässä edellisistä.

Sivuajan kohdassa x0 yhtälöksi saadaan siis s_x0(x)=f'(x0)*(x-x0)+f(x0), auki kerrottuna s_x0(x)=f'(x0)x-f'(x0)x0+f(x0). Sivuajan nollakohdassa s_x0(x) on nolla, joten se saadaan ratkaisemalla x yhtälöstä f'(x0)x-f'(x0)x0+f(x0)=0. Tällöin sivuajan nollakohta on x=x0-f(x0)/f'(x0) eli sivuajan piirtämispiste miinus funktion ja derivaatan arvojen erotus ko. pisteessä.

Exceliin sijoitettuna Newtonin menetelmä on näin ollen hieman kevyempi kuin sijoitusmenetelmä: ehtolauseita ei tarvita, ainoastaan alkuarvaus ja sivuajan nollakohta arvauspisteessä. Askelta kohti suoritetaan periaatteessa vain yksi toimenpide, mutta selvyyden vuoksi käytämme neljää saraketta. Merkitään taas aluksi ruutuun A1 muistiin käsiteltävä funktio. Olkoon se sama kuin edellisessä tehtävässä: f(x)=x^3-2x. Ruutuun C1 kirjoitetaan "arvauspiste", ruutuun D1 "f(arvauspiste)", ruutuun E1 "f'(arvauspiste)" ja ruutuun F1 "sivuajan nollakohta".

Ensimmäinen arvaus voisi olla vaikkapa 1. Kirjoitetaan tämä luku ruutuun C2. Sitten kirjoitetaan funktion arvon laskeva kaava "=C2^3-2*C2" ruutuun D2. Funktio on nyt derivoitava. Tulokseksi saadaan f'(x)=3x^2-2, joten ruutuun E2 kirjoitetaan "=3*C2^2-2", derivaatan arvo arvauspisteessä. Ruutuun F2 kirjoitetaan arvauspisteeseen piirretyn sivuajan nollakohta, joka on äskeisen päättelyn nojalla "=C2-D2/E2". Tämä on itse asiassa seuraava arvauspiste, joten ruutuun C3 kirjoitetaan yksinkertaisesti "=F2". (Tehtävästä oltaisiin selvitty myös ilman F-saraketta kirjoittamalla sivuajan nollakohdan kaava suoraan tähän ruutuun.) Nyt taulukon pitäisi olla jokseenkin tällainen:

Jos saat soluihin eri lukuja kuin kuvassa, tarkista kaavasi! Menetelmä on nyt valmiina; kopioimme taas kaavoja alaspäin. Kopioidaan ensin C3:a valitsemalla ruutu ja vetämällä oikeasta alanurkasta, ja sitten valitaan D2, E2 ja F2 ja kopioidaan niitä saman verran alaspäin. Asetetaan jälleen riittävästi desimaaleja näkymään valitsemalla taulukko ja säätämällä lukujen esitystapaa "Format Cells" -toiminnolla. Tulos on jotain tämän näköistä (jos luvut esitetään kuuden desimaalin tarkkuudella):

Huomataan ensinnäkin, että menetelmä toimii tässä tapauksessa - arvot suppenevat kohti nollakohtaa. Huomataan myös, että menetelmällä päästään hyvin nopeasti hyvin lähelle nollakohtaa. Ei myöskään tarvitse miettiä, suurempi- ja pienempikuin-merkkisääntöjä niin kuin puolitusmenetelmässä. Siksipä Newtonin menetelmää kannattaa käyttää puolituksen sijasta, jos se vain toimii.

Harjoitus 6. Etsi Newtonin menetelmällä kosinifunktion nollakohtia. Käytä apuna Maplea ja piirrä kosinifunktion kuvaaja. Mistä alkupisteistä lähtien löydät mitäkin nollakohtia? Pystytkö sanomaan jotain summittaista sääntöä nollakohtien löytymiselle tässä tapauksessa?

Numeerinen integrointi tarkoittaa määrätyn integraalin arvon approksimoimista (eli arvioimista) menetelmin, jotka eivät vaadi integraalifunktion muodostamista. Tämä on hyödyllistä, koska useiden funktioiden integraalifunktiot ovat erittäin hankalia muodostaa ja käsitellä, eikä niitä tämän kurssin tiedoilla voi saada selville. Numeerisia integrointimenetelmiä on kehitetty lukuisia, mutta tutustumme niistä nyt vain yhteen helppotajuisimmista, ns. puolisuunnikassääntöön.

Määrätty integraali on (x-akselin yläpuolella) sama kuin funktion kuvaajan ja x-akselin väliin jäävä ala integraalin rajojen sisällä. Kaikessa yksinkertaisuudessaan puolisuunnikassääntö sanoo, että eräs approksimaatio tälle alalle on sellaisen puolisuunnikkaan ala, jonka kulmat ovat x-akselilla välin alku- ja loppupisteissä sekä funktion kuvaajalla välin alku- ja loppupisteissä.

Puolisuunnikkaan ala on pohja (tässä a:sta b:hen) kertaa siihen suhteessa suorassa kulmassa olevien sivujen pituuden keskiarvo, siis tässä (b-a)*(f(a)+f(b))/2. Tämä ei ole kuitenkaan vielä kovin tarkka arvio integraalille a:sta b:hen. Arviota voidaan tarkentaa jakamalla integroimisväli kahteen osaväliin, soveltamalla näille väleille erikseen puolisuunnikassääntöä ja laskemalla saadut pinta-alat yhteen. Merkitään osavälin pituutta kirjaimella h. Tällöin h=(b-a)/2 ja puolisuunnikkaiden yhteenlaskettu pinta-ala on h*(f(a)+f(a+h))/2+h*(f(a+h)+f(b))/2.

Integroimisväli voidaan edelleen jakaa useampiin osiin, jolloin h=(b-a)/m, jos m on osavälien lukumäärä, ja yhteenlasketuksi pinta-alaksi saadaan h*(f(a)+f(a+h))/2+h*(f(a+h)+f(a+2h))/2+h*(f(a+2h)+f(a+3h))/2+ ... +h*(f(a+(m-1)h)+f(b))/2. Toteutamme tämän yhteenlaskun nyt Excelin avulla.

Integroidaan esimerkkinä numeerisesti funktiota f(x)=1/2x^2+x. Kirjoitetaan funktion lauseke taas muistiin ruutuun A1. (Tämän funktion integraalifunktiokin on kyllä aika helppo löytää. Mikä se on?) Integroimisvälistä valitaan vain alkupiste; loppupiste voidaan vapaasti valita kohta muodostettavasta taulukosta. Valitaan alkupisteeksi 1.

Ruutuun C1 voimme nyt kirjoittaa "alkupiste", ruutuun D1 "osavälin pituus", ruutuun E1 "osavälien rajapisteet", ruutuun F1 "funktion arvo pisteessä", ruutuun G1 "puolisuunnikkaan ala" ja ruutuun H1 "Integraali". Tässä tarkastelussa määritämme käsin alkupisteen ja osavälin pituuden. Olisi mahdollista laatia taulukko myös niin, että tarkasteluväli olisi etukäteen määrätty ja osavälien määrä annettaisiin käsin.

Sijoitetaan ruutuun C2 alkupisteemme arvo 1 ja D2:een aluksi osavälin pituudeksi 0,5. Ruutuun E2 sijoitamme ensimmäisen osavälin alkupisteen, joka on sama kuin koko tarkastelualueen alkupiste, siis "=C2". Ruutuun E3 sijoitetaan edellinen arvo + osavälin pituus, siis "=E2+$D$2". Huomaa dollarimerkit kaavassa! Ne takaavat, että osavälin pituus luetaan aina samasta ruudusta huolimatta siitä, mihin tämän ruudun kaavaa kopioidaan. Dollarimerkit siis estävät Exceliä muuttamasta kaavan syöttöruutua "älykkäästi" kaavaa kopioitaessa. Ensimmäinen merkeistä kiinnittää syöttöruudun sarakkeen ja toinen rivin.

Ruutuun F2 laskemme funktion arvon viereisen ruudun osoittamassa pisteessä. Sijoitamme siis funktion lausekkeeseen viereisen ruudun nimen, näin: "=0,5*E2^2+E2". (1/2=0,5)

Ruudun G2 jätämme tyhjäksi: mitään puolisuunnikasta ei ole vielä muodostunut, koska on vasta yksi arvopiste. Kirjoitamme sarakkeen ensimmäisen kaavan ruutuun G3. Tällä kaavalla kuvaamme sen puolisuunnikkaan alaa, joka muodostuu ensimmäiselle osavälille. Sijoittamalla alan kaavaan vastaavat arvoruudut saadaan kaava "=$D$2*(F2+F3)/2". Tässä siis kerrotaan osavälin pituudella edellisen osavälin funktion arvojen keskiarvo. Huomaa, että osavälin pituuden sisältävä ruutu on taas kaavassa kiinnitettävä dollarimerkeillä!

Lopulta kirjoitamme ruutuihin H3 ja H4 tarvittavat kaavat numeerisen integraalin laskemista varten. H3:ssa integraali on sama kuin ensimmäisen puolisuunnikkan ala, siis "=G3". H4:ssä pitää edellinen arvo laskea yhteen seuraavan puolisuunnikkaan alan kanssa. Se tulee ruutuun G4, joten kaava "=H3+G4" kerryttää seuraavan puolisuunnikkaan alan jo laskettuun arvoon. Taulukon pitäisi nyt olla tämän näköinen:

Taulukon arvot eivät ole vielä oikeat; osa kaavoista viittaa tyhjiin ruutuihin, jotka täytetään vasta nyt kaavoja kopioimalla. Siispä kopioidaan. Ensin merkataan solu E3 ja kopioidaan sitä alaspäin, sitten F2:ta, sitten G3:a ja lopulta H4:ää. Otetaan esiin riittävän monta desimaalia (tässä olen tyytynyt kahteen; arviot eivät kuitenkaan ole älyttömän tarkkoja) ja saadaan lopullinen taulukko:

Nyt oikeanpuolimmaisesta sarakkeesta voi lukea numeerisen integraalin 1:stä mihin tahansa sarakkeen E pisteeseen. Taulukko muuttuu, jos vaihdat ruutuihin C2 ja/tai D2 eri integroimisvälin alun ja osavälin leveyden. Kokeile! Huomaa, että mitä lyhyempi osaväli on, sitä pidemmälle joudut kopioimaan kaavoja saadaksesi selville integraalin johonkin asti. Toisaalta arvo tarkentuu.

Tämä menetelmä antaa oikean integraalin myös tapauksessa, jossa funktio saa negatiivisia arvoja, sillä "puolisuunnikkaan pystyreunalle" tulee tällöin negatiivinen pituus, jolloin "pinta-alaksikin" voi tulla negatiivinen luku. Jos siis integroit numeerisesti saadaksesi selville käyrän ja x-akselin välisen pinta-alan, sinun on tätä menetelmää käyttäessäsi muistettava tutkia erikseen integroimisvälin alueita, joilla funktion arvo saa eri merkit ja summata negatiivisten integraalien vastaluvut positiivisten kanssa!

Harjoitus 7. Integroi numeerisesti välillä [1, 3] funktio exp(sqrt(x)), missä sqrt tarkoittaa neliöjuurta. Funktioiden exp ja sqrt nimet ovat samat Excelissä. Muodosta integraali neljällä, kahdeksalla ja 32 osavälillä. Mitä huomaat integraalin tarkkuudesta? Yritä Maplella muodostaa tehtävän funktiosta integraalifunktio. Miksi Numeerinen integrointi on tässä hyödyllistä?

Harjoitus 8. Selvitä graafista integraalia apuna käyttäen ja kokeilemalla, millä integroimisvälin alulla funktion f(x)=x^3-2x integraaliksi saadaan 0, jos integroimisvälin loppu on a) 3, b) 5 tai c) -3. C-kohdassa aseta osavälin pituudeksi negatiivinen luku! Mitä havaitset? Onko tämä uskottavaa? Mitä se kertoo funktiosta? Miten c-kohdassa integraalin arvo muodostui, kun integroitiin "takaperin"?

Tässä tutustumme pinnallisesti neljään tilastolliseen perustunnuslukuun, opimme laskemaan ne Excelillä ja piirrämme lineaarisen ja eksponentiaalisen regressiokuvaajan.

Ensimmäinen tunnuslukumme on keskiarvo. Tämä luku soveltuu tilastollisille aineistoille, joiden yksittäiset alkiot ovat numeroarvoja. Keskiarvo lasketaan kaavalla Σ(x_i)/n, missä x_i:t ovat tilastollisen aineiston yksittäiset arvot ja n arvojen määrä. Iso sigma kuvaa summaa, ja sanallisesti keskiarvon voikin ilmaista aineiston arvojen summana jaettuna arvojen määrällä. Esim. tulojakaumassa keskiarvo kertoo, kuinka paljon rahaa aineiston ihmisillä olisi henkilöä kohti, jos rahat jaettaisiin tasan. Keskiarvo on matemaattisesti helppokäyttöinen ja ominaisuuksiltaan selkeä tunnusluku, jota käytetään melkein kaikessa tilastollisessa laskennassa (esim. kahta tai useampaa eri aineistoa verrattaessa). Periaatteessa samalla kaavalla lasketaan tilastosta myös ns. odotusarvo, jolla kuvataan keskimääräistä odotettavissa olevaa uutta arvoa, jos tilasto käsitetään jonkin satunnaismuuttujan ilmenemäksi.

Keskiarvo on kuitenkin leimallisesti koko aineiston abstrakti ominaisuus. Sillä saattaa olla aineiston esitystavasta riippuen hyvinkin heikko kyky kuvailla aineistoa. Esim. jakaumassa, jossa hyvin pieniä ja hyvin suuria arvoja on paljon, mutta keskisuuria ei lainkaan, yksikään aineiston arvo ei muistuta läheskään keskiarvoa. Keskiarvo kuvaa aineistoa parhaiten, jos aineiston jakauma on symmetrinen ja kasautunut keskiarvon lähistölle kuten esim. normaalijakauma.

Keskiarvo lasketaan Excelissä funktiolla AVERAGE. Syötämme ruutuihin A1-A10 nyt seuraavan aineiston:

Sitten kirjoitamme ruutuun C1 aineiston keskiarvon kaavan: "=AVERAGE(A1:A10)". Kaksoispiste tarkoittaa kaikkia ruutuja, jotka jäävät alku- ja loppuruudun väliin. (Esim. A1:B10 tarkoittaisi ruutuja A1:stä A10:een ja ruutuja B1:stä B10:een!) Ruutuun pitäisi tulla keskiarvo 4,9.

Seuraavaksi laskemme aineiston moodin eli tyyppiarvon. Moodi on se arvo, joka esiintyy aineistossa useimmin. Moodi soveltuu myös sellaisten aineistojen kuvailuun, joissa arvot eivät ole numeerisia. Esim. suomalaisten siviilisäätymoodi on se siviilisääty, johon suurin osa suomalaisista kuuluu. Moodi voi poiketa keskiarvosta hyvinkin paljon, ja se kuvaa aineistoa usein hyvin tilanteissa, joissa hyvin suuressa aineistossa arvot selkeästi keräytyvät tiettyihin kohtiin. Lasketaan ruutuun C2 aineistomme moodi kaavalla "=MODE(A1:A10)". Tuloksen pitäisi olla 3.

Mediaani on kolmas havainnollinen aineiston "keskiluku", joka kertoo, minkä arvon ala- ja yläpuolella on yhtä monta aineiston arvoa. Mediaani siis jakaa aineiston keskeltä kahtia. Mikäli aineiston arvojen lukumäärä on parillinen, mediaani on kahden keskimmäisen luvun keskiarvo (siis kun aineisto on ensin järjestetty suuruusjärjestykseen). Mediaani kertoo esim. tulojakaumasta usein enemmän kuin keskiarvo, sillä keskiarvoa saattavat painaa kovinkin ylös yksittäiset hyvin suuret arvot muuten pieniarvoisessa aineistossa. Tavallaan mediaani tällöin kertoo, millainen on "keskiverto" tulonsaaja. Laskemme aineistomme mediaanin kaavalla "=MEDIAN(A1:A10)" ruutuun C3. Tulos: 4,5.

Neljäs ja viimeinen tunnuslukumme ei ole "keskiluku", kuten muut kolme, vaan ns. hajontaluku, joka kertoo, kuinka paljon aineiston arvot poikkeavat keskiarvosta. Hajontalukuja voi laskea useilla tavoilla, mutta matemaattisesti käyttökelpoisin on ns. keskihajonta (standard deviation), jota toisinaan myös kutsutaan keskivirheeksi tai keskipoikkeamaksi (näitä termejä käytetään kuitenkin joskus ristiin muiden käsitteiden kanssa, joten keskihajonta lienee varmin tapa puhua ko. luvusta). Keskihajonta lasketaan korottamalla jokaisen arvon ja aineiston keskiarvon erotus neliöön, summaamalla nämä neliöt, jakamalla aineiston määrällä vähennettynä yhdellä ja ottamalla koko jutusta neliöjuuri. Menettely muodostaa luvun, joka kuvaa aineiston arvojen poikkeamaa keskiarvosta, mutta käyttää siihen normaalista summaamisesta poikkeavaa ns. 2. normin mukaista menettelyä, joka helpottaa luvun käyttöä tilastollisissa testeissä. Laskemme aineistomme keskihajonnan ruutuun C4 kaavalla "=STDEV(A1:A10)". Tulokseksi saamme 2,558211. Keskihajontaa käytetään mm. yksinkertaisessa t-testissä, jossa verrataan kahden aineiston keskiarvoja ja keskihajontoja. Karkeasti ottaen t-testin periaate on tämä: mitä suurempi on keskiarvojen erotus ja mitä pienemmät keskihajonnat, sitä merkittävämpi on aineistojen ero toisiinsa nähden.

Mikäli tilaston arvot osoittavat taipumusta kehittyä johonkin tiettyyn suuntaan jollakin tietyllä tavalla, voidaan mahdollisia tulevia arvoja yrittää ennustaa muodostamalla funktio, joka kuvaa arvojen käyttäytymistä. Tällöin sovitetaan arvopisteisiin parhaiten sopiva käyrä, jota kutsutaan regressiokäyräksi tai trendiviivaksi. Funktiotyyppi, jota arvojen epäillään noudattavan, on arvattava esim. tilaston kuvaajaa katsomalla. Oikeaa funktiota ei voi mikään ohjelma varmuudella sanoa, joskin on olemassa joitakin testejä sille, kuinka luotettavana saatua regressiota voidaan pitää. Piirrämme seuraavassa Excelin automaattisella trendiviivatoiminnolla kuvaajat lineaarisesti ja eksponentiaalisesti kehittyvään (tai sellaiseksi oletettuun) aineistoon. Regressiokuvaajan laskeminen on pitkällinen toimenpide, joka on syytä jättää tietokoneen suoritettavaksi.

Ensimmäisessä tapauksessa mittaamme auton nopeutta tasaisin väliajoin, kun autoon vaikuttaa jokin voima, esim. kiihdyttävä moottori. Sijoitamme A-sarakkeeseen ajanhetket 0-5 ja B-sarakkeeseen auton nopeudet seuraavasti:

Nyt piirrämme pistediagrammin, jossa aika-akseli on alareunassa ja nopeusakseli sivureunassa. Tämä voidaan tehdä valitsemalla taulukko (siis solut A1:stä B6:een) ja painamalla graafintekonappia, valitsemalla taulukkotyypiksi "XY (Scatter)" ja painamalla suoraan Finish-nappia. Näin saadaan (muotoiluiltaan tosin karkea) kaavio, joka esittää mitatut auton nopeudet eri ajanhetkillä. Kuvasta nähdään, että nopeus kasvaa melkein lineaarisesti eli suoran f(x)=kx+a mukaisesti, missä k ja a ovat vakioita. Todennäköisesti autoon siis vaikuttaa melko tasainen voima ja voimme olettaa poikkeamien tasaisesta kiihtymisestä olevan satunnaisia tai johtuvan mittausvirheistä. Sovitamme nyt regressiosuoran kuvaamaan kuvitellun auton nopeusfunktion kulkua.

Painetaan kuvaajan jotain arvopistettä, jolloin kaikki arvopisteet saavat päälleen mustat neliöt. Painetaan sitten arvopisteen kohdalla hiiren oikeaa nappia ja valitaan avautuvasta pop-up-valikosta "Add Trendline...". Esiin tulee valintaikkuna, jossa on välilehdet Type ja Options. Koska haluamme lineaarisen regressiokuvaajan, valitsemme tyypiksi "linear". Options-välilehdestä valitsemme kohdan "Display equation on chart", jolla saamme regressiosuoran funktion määrittelyn esiin kuvaajaan. Tämän jälkeen painetaan "OK". Kuvaajaan piirtyy arvio siitä, miten auton nopeus suunnilleen kehittyy (Tätä olisi voinut ekstrapoloida Options-välilehden Forecast-kohdasta). Kuvaajan viereen ilmestyy funktio (y = 2x + 10), jolla voidaan laskea arvioita auton tuleville nopeuksille, jos kehitys pysyy samansuuntaisena. Esim. arvioitu nopeus hetkellä 10 olisi 2*10+10=30.

Samaan tapaan voidaan laskea eksponentiaalinen tai mm. polynominen tai logaritminen regressio, riippuen siitä mitä funktiota meidän on parhaiten syytä olettaa tilaston arvojen seuraavan. Lineaarinen ja eksponentiaalinen ovat käytännössä ehkä yleisimmät, sillä meillä saattaa olla esitieto tai- hypoteesi mitattavaan ilmiöön vaikuttavasta vakiotekijästä (lineaarinen tapaus) tai ilmiön muutosnopeuden riippumisesta ilmiöstä itsestään (eksponentiaalinen tapaus). Kuitenkin esim. jos äskeisessä tapauksessa olisi tarkasteltu auton sijainteja eri aikoina, niitä olisi parhaiten sopinut kuvaamaan toisen asteen kuvaaja, koska sijainti on nopeuden (joka oli siis ensimmäistä astetta) integraali.

Muutetaan nyt äskeisen taulukon arvot kuvaamaan erään bakteeripopulaation havainnoista arvioitua kasvua ajanhetkinä 0-5, seuraavasti:

Piirretään tästä uusi XY-kuvaaja ja tarkastellaan sen pisteitä. Pisteiden asettuminen näyttää eksponentiaaliselta, samaten tilanne on mahdollinen eksponentiaalisen kasvun tilanne: jokainen uusi bakteeri pyrkii lisääntymään. Tällä kertaa piirrämme eksponentiaalisen regressiokäyrän menetellen muuten samoin kuin viimeksi, mutta valiten "Add Trendline" -ikkunan Type-välilehdestä tyypin "Exponential".

Kuvan pitäisi nyt näyttää tältä. Käyrä sopi pisteisiin varsin hyvin eli ilmeisesti kysymys on eksponentiaalisesta kasvusta. Bakteeripopulaation kokoa hetkellä x voi arvioida sijoittamalla kuvan kaavaan x:n paikalle ajanhetki ja ratkaisemalla y.

Harjoitus 9. Laadi hyvin tuntemistasi kanssaopiskelijoista ikätilasto. Mikä on tilaston keskiarvo? Entä moodi, mediaani ja keskihajonta? Onko moodin ja keskiarvon tai mediaanin ja keskiarvon poikkeama suuri? Mitä nämä poikkeamat mielestäsi kuvastavat? Entäpä keskihajonta?

Harjoitus 10. Taimen pituudet peräkkäisinä päivinä (mitattuna klo 12 päivällä) olivat 1,2cm, 1,8cm, 2,3cm, 3,0cm, 3,7 cm ja 4,3cm. Muodosta aineistosta taulukko ja kuva. Minkälaisen regressiokuvaajan sijoittaisit kuvaajaan? Jos ensimmäinen päivä oli numero 0, kuinka pitkä arvioit taimen olevan päivänä 20 regressiota piirtäessäsi saamasi funktion mukaan?

Tutustutaan matriisien perusoperaatioihin Excelillä.

Eräs Excelin vahvuus on siinä, että kaavoja voidaan kopioida ruudusta toiseen helposti niin, että viittaukset muihin soluihin siirtyvät mukana. Tämän avulla matriisien yhteenlaskun ja skalaarikertolaskun suorittaminen on äärimmäisen helppoa.

Luodaan kaksi matriisia yksinkertaisesti kirjoittamalla lukuja taulukkoon. (Mitäpä muutakaan matriisi on kuin lukuja taulukossa?)

Lasketaan ensin nämä matriisit yhteen. Yhteenlasku tapahtuu alkioittain, joten kirjoitetaan tulosmatriisin ensimmäiseen soluun ensimmäisten alkioiden summa: =A2+E2. Tämän jälkeen kopioidaan kaavaa oikealle ja alas koko matriisin kokoiseksi. Excel muuttaa viittaukset juuri halutulla tavalla.

Kerrotaan sitten matriisi A luvulla 7. Kirjoitetaan jälleen haluttu kaava =7*A2 tulosmatriisin ensimmäiseen soluun ja kopioidaan matriisin kokoiseksi.

Matriisien kertolasku on hieman vaikeampi operaatio. Siihen Excel tarjoaa valmiin funktion MMULT. Kaava =MMULT(...) on niin sanottu taulukkokaava (array formula), jonka tuloksen näyttämiseen tarvitaan useampi taulukon solu. (Tavallisen kaavan tuloshan näkyy yhdessä solussa.) Taulukkokaavojen syöttäminen ei ole aivan ongelmatonta.

Matriisit A ja B ovat sellaisia, että ne voidaan kertoa keskenään. Kirjoitetaan tulosmatriisin ensimmäiseen soluun kaava =MMULT(A2:C4;E2:G4) ja painetaan Enter. Tuloksesta näkyy nyt vain yksi solu. Tämän jälkeen suoritetaan peräkkäin seuraavat toimenpiteet:

1. maalataan tulosmatriisin tarvitsema alue,
2. painetaan F2,
3. painetaan (yhtä aikaa) Ctrl+Shift+Enter.

Taulukkokaavan tunnistaa siitä, että muokkausrivillä olevan kaavan ympärillä näkyy aaltosulut { }. Taulukkokaavoja ei voi muokata niiden luomisen jälkeen. Jos näin yrittää tehdä, ohjelma antaa virheilmoituksen: "You cannot change part of an array." Tästä tilanteesta pääsee pois painamalla Esc. Jos taulukkokaavan on syöttänyt väärin, solu täytyy tyhjentää ja kaava kirjoittaa uudestaan.

Käänteismatriisin laskemiseksi Excelissä on kaava MINVERSE. Tämän on myös taulukkokaava, jota käytetään samalla tavoin kuin kertolaskukaavaa. Lasketaan esimerkiksi A:n käänteismatriisi. Kirjoitetaan sitä varten kaava =MINVERSE(A2:C4), maalataan sopivan kokoinen (3x3) alue, painetaan F2 ja lopulta Ctrl+Shift+Enter. Käänteismatriisi ilmestyy soluihin.

Taulukkokaavoja voi kopioida samalla tavoin vetämällä kuin tavallisiakin kaavoja. Lasketaan esimerkiksi matriisin A potensseja. Nämä määritellään samalla tavoin kuin luvuillakin, eli A^2=AA, A^3=AAA, jne. Huomaa kuitenkin, että vain neliömatriiseja voidaan korottaa potenssiin.

Voimme laskea A:n peräkkäisiä potensseja kertomalla edellinen potenssi aina uudestaan A:lla. Kirjoitetaan sitä varten aivan A:n alapuolelle (jättämättä riviäkään väliin) kaava, jossa yläpuolella oleva matriisi kerrotaan A:lla. Kaavaksi tulee siis (kuvan mukaan) =MMULT($A$2:$C$4;A2:C4). Huomaa, että ensimmäiseen viittaukseen tulee dollarimerkit. Tämä sen takia, että kaavaa kopioitaessa syntyvissä kaavoissa kerrottaisiin aina alkuperäisellä matriisilla A.

Tämän jälkeen maalataan sopiva alue (3x3-matriisi), ja painetaan F2 ja Ctrl+Shift+Enter. Matriisin pitäisi ilmestyä näkyviin. Sitten vain kopioidaan kaavaa alaspäin vetämällä, jolloin syntyy matriisin potensseja.

Harjoitus 11. Tarkastellaan matriiseja

    |  3 -4  2  |              |  1  0 -2 |
A = | -1  0  1  |    ja    B = | -3 -4 -3 |   .
    |  2  1  -3 |              |  2 -5  2 |

Harjoitus 12. Ratkaise yhtälöryhmä

 16a +  8b +  4c + 2d + e = -10
 81a - 27b +  9c - 3d + e = -135
   a -   b +   c -  d + e = 5
 16a -  8b +  4c - 2d + e = -18
256a - 64b + 16c - 4d + e = -450

Harjoitus 13. Neliömatriisin determinantti on matriisia kuvaava luku, joka voidaan laskea Excelin kaavalla MDETERM (tämä ei siis ole taulukkokaava). Tutki helppojen 2x2-matriisien avulla, miten kahden matriisin tulon determinantti riippuu tekijämatriisien determinanteista. Entä miten käänteismatriisin determinantti riippuu alkuperäisen matriisin determinantista?

Maple on sekä symboliseen että numeeriseen laskentaan sopiva matematiikkaohjelma. Sen pääpaino on kuitenkin symbolisessa laskennassa. Maple osaa suorittaa toisinaan hyvinkin vaikeita symbolisia matemaattisia toimituksia.

Maple löytyy ainakin GIS-luokan, keskustan ja Kumpulan laitosten koneista. Olen kuullut, että myös biotieteillä olisi jossakin Maple, mutta en ole varmistanut tätä itse. Jollei Maplea ole käyttämääsi koneeseen asennettu, sitä voi etsiskellä "Installations"-kansiosta ja asentaa. Maplea voi käyttää eri käyttöliittymillä, joista nyt käytämme Maplen Classic Worksheet -käyttöliittymää. Tämä käyttöliittymä on luotettavampi ja varmempi kuin Maplen varsinainen "Maple 10" -käyttöliittymä (joka olisi kyllä graafisesti näyttävämpi). Tämä käynnistetään kuvakkeesta "Classic Worksheet Maple". (Muualla kuin GIS-luokassa käytössä saattaa olla Maple 9.5, joka on melko samanlainen.)

Työtilan alussa on uusi tyhjä kenttä merkittynä hakasesta ja nuolesta koostuvalla kehotteella [>. Työtilaan voit kirjoittaa periaatteessa millaisia tahansa matemaattisia lausekkeita tai Maplen komentoja. Kun painat kentässä ENTERiä, Maple suorittaa komennot ja laskut, joiden kohdalla kursorisi välkkyy, ja siirtyy eteenpäin. Maple antaa tulosteensa, yleensä siis laskujen vastaukset, sinisellä värillä. Huomaa, että Maplen vastaukset muistuttavat hieman enemmän perinteistä matemaattista kirjoitusasua kuin käyttäjän kirjoittamat, Maplelle ymmärrettävät lausekkeet - esim. käyttäjä ei voi jättää kertomerkkiä pois laskulausekkeista.

Maplelle syötettävien lausekkeiden ja komentojen yhteydessä on syytä huomata seuraavat seikat:

• Kertomerkit kannattaa matemaattisissa lausekkeissa kirjoittaa näkyviin, vaikkeivät ne Maplen vastauksissa näykään. (Jotkut käyttöliittymät ymmärtävät kyllä ilmauksen 3x tarkoittavan samaa kuin 3*x, mutta esim. ilmauksia kx tai x(x+1) nekään eivät käsittele oikein. Siispä kirjoitamme k*x ja x*(x+1).)
• Maple käyttää desimaalierottimena pistettä (toisin kuin käyttämämme Excel suomalaisilla asetuksilla).
• Mikäli Maple ei tunnista sille annettua merkkiä tai merkkiyhdistelmää joksikin määrätyksi komennoksi, operaattoriksi tai numeroksi, se olettaa, että kysymyksessä on muuttuja. Huomaa, että Maple erottaa pienet kirjaimet isoista ja pitää niitä eri merkkeinä!
• Jokaisen suoritettavn rivin loppuun on lisättävä puolipiste. Ilman puolipistettä Maple ei suostu laskemaan, vaan vaatii sitä.
• Minne tahansa työtilassa voi mennä tekemään korjauksia (liikuttamalla kursoria tai klikkaamalla hiirellä) ja kaavat tai komennot voi suorittaa uudelleen menemällä niiden riville ja painamalla ENTER. Työtilan sisältöä voi myös kopioida esim. merkkaamalla hiirellä kopioitavat asiat, klikkaamalla oikeaa nappia ja valitsemalla "Copy". Tämän jälkeen kopioidut asiat voi liittää haluamaansa paikkaan klikkaamalla ko. paikassa jälleen oikeaa nappia ja valitsemalla "Paste". Myös Maplen vastauksia voi kopioida.

Maple laskee tavalliseen tapaan peruslaskutoimitukset summan, erotuksen, tulon ja osamäärän (merkit +, -, *, /). Kokeillaan laskemalla 15*263.

15*263; [ENTER]

Maple ilmoittaa tuloksen 3945. 1.2*5.6 puolestaan on Maplen mukaan 6.72. 1/2:n tuloksen Maple taas ilmoittaa murtolukumuodossa. On huomattava, että Maple laskee oletusarvoisesti kaikki jako- ja juurilaskut (ja kaikki muutkin laskut) symbolisesti, siis ei desimaaliluvuilla kuten laskimet, vaan tarkoilla arvoilla (paitsi jos käyttäjän syöttämät luvut ovat desimaalilukuja). Siksi murtoluvut pysyvät Maplen laskuissa murtolukuina, juuret juurina ja irrationaaliluvut irrationaalilukuina, eikä niitä ilmoiteta laskujen tuloksissa likiarvoina.

Potenssiin korotus tehdään Maplessa operaattorilla ^, jonka saa näppäinyhdistelmällä SHIFT-¨ ja painamalla tämän jälkeen välilyöntiä (tai jo seuraavaa numeroa t. kirjainta, jolloin näkyviin tulevat sekä operaattori että seuraava merkki). Neliöjuuren voi ottaa komennolla sqrt(juurrettava) ja mielivaltaisen juuren korottamalla murtopotenssiin tai komennolla root[juuren luku](juurrettava) (esim. kuutiojuuri neljästä saataisiin kaavalla root[3](4)). Huomaa, että Maple voi esim. juurilaskuissa ja vallankin mutkikkaammissa toimituksissa antaa kompleksiratkaisuja, jotka tunnistaa mukana olevasta isosta I-kirjaimesta. Tämä on Maplessa ns. imaginääriyksikön symboli, eikä sitä käytetä muuttujan nimenä. Koska kurssimme koskee reaalisia funktioita, voimme jättää kompleksivastaukset kylmästi huomiotta.

Desimaalilikiarvon Maplen antamalle murto- tai irrationaalivastaukselle saa evalf-funktiolla. Kirjoitetaan

evalf(sqrt(2)); [ENTER]

Näytölle tulee kakkosen neliöjuuren likiarvo kymmenen desimaalin tarkkuudella. (Tämä on Maplen oletustarkkuus, jota voi halutessaan säätää digits-komennolla.)

Usein on käytännöllisempää saada desimaalilikiarvo yksinkertaisesti syöttämällä joku lähtöarvoista desimaalilukuna. Saman tuloksen kuin edellinen esimerkki antaisi myös laskutoimitus sqrt(2.), missä Maple tulkitsee luvun "2." desimaaliluvuksi 2.0.

Logaritmien laskeminen Maplella onnistuu komennolla log. Pelkkä log(luku) tarkoittaa Maplessa luonnollista logaritmia, jonka kantaluku on e. Mielivaltainen logaritmi ilmaistaan muodossa log[a](luku), missä a on logaritmin kantaluku. Hakasulkeet löytyvät painamalla pohjaan "Alt Gr" -näppäin ja sitten 8:aa ja 9:ää. Kymmenkantaiselle logaritmille Maplessa on oma komento log10. Logaritmit ovat yleensä irrationaalisia, joten Maplen vastaus vaikkapa käyttäjän lausekkeeseen "log(5)" on yksinkertaisesti "log(5)". Logaritmin desimaalilikiarvo saadaan taas kirjoittamalla viitosen tilalle "5." tai koko lauseke evalf-funktion jälkeen sulkeisiin.

Sini, kosini ja tangentti lasketaan Maplessa funktioilla sin, cos ja tan. Arvot ovat jälleen tavallisesti irrationaalisia, joten vastauksena vaikkapa lausekkeeseen "sin(3)" Maple antaa "sin(3)". Maplessa on määriteltynä vakio π, joka ilmaistaan "Pi". Esimerkkinä Maplen symbolisen laskennan älykkyydestä voimme ottaa sinin ja kosinin piistä:

sin(Pi);


                                                     		0

cos(Pi);


								-1

Maple "ymmärtää" piin merkityksen trigonometrisissä (ja monissa muissakin) yhteyksissä ja osaa laskea sen avulla tarkkoja arvoja. Maple osaa myös ilmaista monen laskutoimituksen tuloksen piin, ei piin likiarvon avulla. Huom! Maple laskee trigonometriset funktiot radiaaneilla. Asteet voi muuttaa radiaaneiksi kertomalla piillä ja jakamalla 180:llä. (Käytä tällöin Maplessa "Pi":tä jos haluat tarkan arvon!)

Matemaattiselle vakiolle e Maplella ei ole varsinaista omaa merkintää, vaan sitä käsitellään eksponenttifunktion arvona kohdassa 1. Tähän palaamme seuraavassa luvussa.

Maple noudattaa normaaleja laskujärjestyssääntöjä: ensin logaritmit ja trigonometriset funktiot, sitten potenssit, sitten kerto- ja jakolaskut ja lopuksi yhteen- ja vähennyslaskut. Laskujärjestystä voi muuttaa sulkeilla (), joita käytetään tavalliseen tapaan. Käytämme vain tavallisia sulkuja määrittämään laskujärjestystä, jotta vältämme sekaannukset joidenkin Maplen komentojen käyttämien erikoissulkujen kanssa.

Maple-työtilan - eli kaiken mitä olet tehnyt - voi tallentaa kuten minkä tahansa dokumentin valitsemalla File-valikosta komennon "Save as...". Ennestään tallennetun työtilan voi tallentaa vanhan päälle samasta valikosta Save-komennolla. Työkalurivistä löytyvä "!!!"-nappi voi myös joskus olla hyödyksi: se lukee ja suorittaa uudelleen koko työtilan laskut ja komennot. Lisäksi Maplessa on erittäin laaja, syvällinen ja toimiva opastus (Help-valikosta), jonka käyttäminen tosin vaatii aluksi pientä totuttelua.

Ennen kuin siirrymme käsittelemään funktioita, mainitsen vielä erään olennaisen Maplen ominaisuuden:
Vaikka Maple käsittelee tuntemattomia kirjaimia ja kirjainyhdistelmiä (siis muita kuin Maplen funktioita ja komentoja) normaalisti tuntemattomina ja laskee niillä aivan kuin laskemme normaalisti algebraa, voimme halutessamme myös sijoittaa muuttujalle arvon. Sijoitusoperaattorina on ":=". Tätä ei pidä sekoittaa yhtäsuuruusmerkkiin "=", jota voidaan käyttää vaikkapa loogisissa testeissä ja monenlaisissa komennoissa. Sijoitamme vaikkapa muuttujalle t arvon 4:

t:=4;


								4

Tämän jälkeen voimme laskea muuttujalla kuin se olisi ko. luku:

5*t;


								20

Harjoitus 1. Laske Maplella tarkat arvot ja likiarvot: 285-766, Pi*(-11.3), 14^(4-1), 122/739, sqrt(10), 8^(2/3), 8^2/3, log[2](16), log(-cos(Pi)), sin(Pi/4), tan(1). Kokeile numeroiden muuttamista kenttiin ja laske uudelleen. Tallenna.

Harjoitus 2. Syötä Mapleen lausekkeet a+b, a*b/a, a^(6*b/3*b), sin(a-a). Paina joka lausekkeen jälkeen ENTER. Miten Maple toimii? Sijoita sitten a:han luku 2 ja b:hen 3. Mene takaisin edellisiin laskuihin a:lla ja b:llä ja laske ne uudelleen (painamalla ENTER joka kohdassa). Mitä saat tulokseksi?

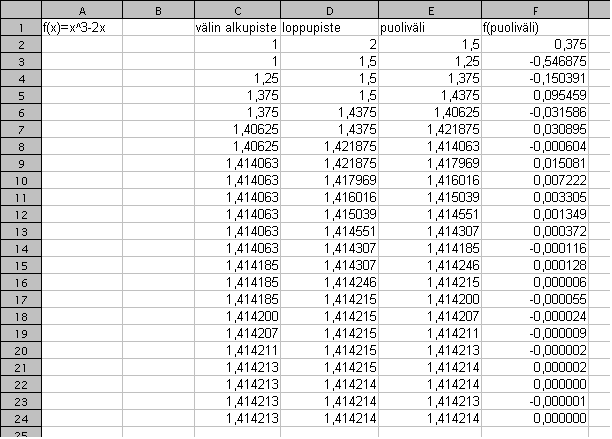
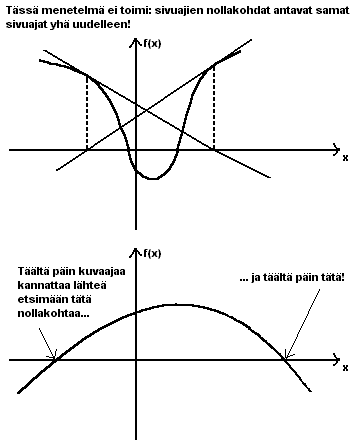
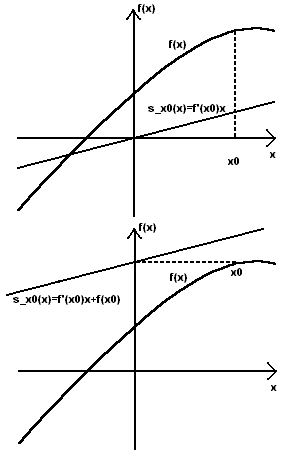
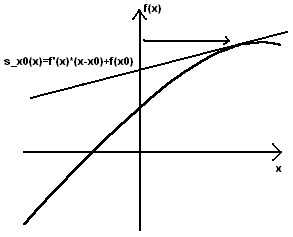
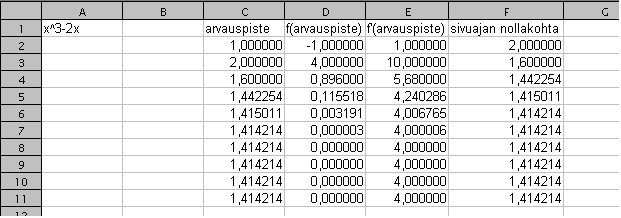
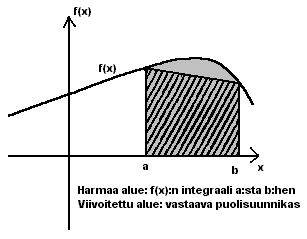
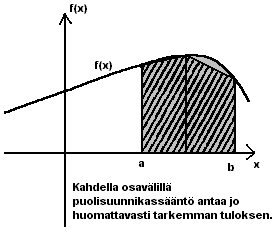
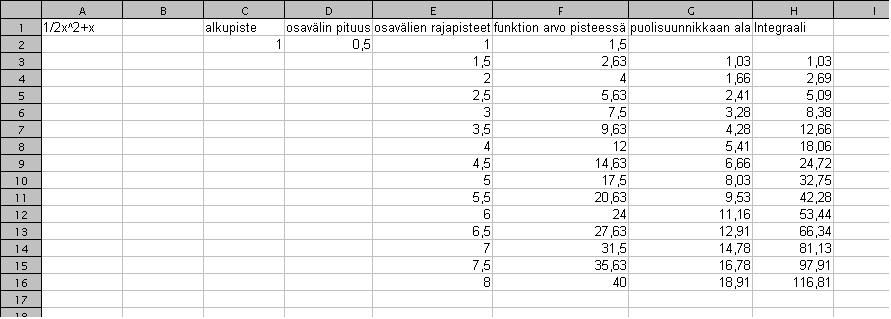
Funktiot voi määritellä Maplessa symbolisesti sijoitusoperaattorin ja "nuolen" (->) avulla. Tätä nuolta ei pidä sekoittaa luennoilla ja materiaalissa funktion määrittely- ja maalijoukosta kertovan merkinnän nuoleen. Maplessa funktion määrittelyyn käytetty nuoli merkitsee samaa kuin toisinaan matemaattisessa tekstissä esiintyvä nuoli, jonka alussa on pystyviiva (). Maplessa nuolen alkuun tulee siis muuttuja ja loppuun riippuvuusehto. 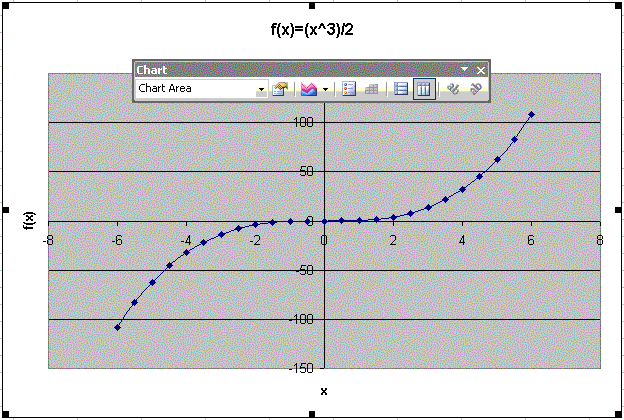Määrittelemme nyt funktion f(x)=x^3-2x.

f := x -> x^3-2*x; (Enää en merkitse ENTERin painalluksia näkyviin.)

Huomaa, että funktion nimen jälkeen ei merkitä sulkuihin muuttujaa. Funktio toimii nyt millä muuttujilla tai luvuilla tahansa. Kokeillaan:

f(3);


								21

f(t-2);
								(t-2)3-2t+4

Huomaa, että Maple ei kerro auki eikä sievennä lausekkeita automaattisesti. Sievennys sujuu simplify(sievennettävä)-komennolla ja auki kertominen expand(auki kerrottava) -komennolla. Voit kokeilla tätä. (Tässä tapauksessa molemmat komennot antavat saman tuloksen.)

Voit myös määritellä vakiofunktion:

f := x -> 3;

Tällöin funktio saa saman arvon riippumatta muuttujasta.

f(Pi*I);


								3

Tutkitaan nyt muutamia funktioita Maplella. Muodostetaan funktio f(x)=2x² ja piirretään sen kuvaaja.

f := x -> 2*x^2;

Kuvaaja piirretään komennolla "plot". Plotin jälkeen tulee suluissa joukko argumentteja, joista tässä käytämme kahta. Aluksi kirjoitetaan piirrettävän funktion nimi ja muuttuja sulkuihin (tässä f(x)) tai lauseke, sitten x-akselin arvot, joiden alueella kuvaaja piirretään. Kun haluamme kuvaajan x:n arvoilla -3:sta 3:een, komento on kokonaisuudessaan:

plot(f(x), x=-3..3);

Kuvaaja on ylöspäin aukeava paraabeli, jonka huippu on origossa. Maple skaalaa pysty- eli y-akselin automaattisesti, mutta aina tulos ei ole paras mahdollinen. Muodostetaan nyt funktio g(x)=(5*x^2+2*x)/(3*x^2-x) ja piirretään sen kuvaaja.

g:=x->(5*x^2+2*x)/(3*x^2-x);

(Välilyöntien käyttö Maplessa on yhdentekevää; niitä on syytä käyttää silloin kun ne selventävät asiaa kirjoittajalle itselleen.)

Lisätään plot-komentoon nyt kaksi argumenttia: Funktion ja x:n arvojen jälkeen ilmaistaan kuvaajassa näytettävän alueen mitat pystysuunnassa. Neljäs argumentti "discont=true" käskee Maplea etsimään funktion mahdolliset epäjatkuvuuskohdat (discontinuity) sekä kohdat, joissa funktiota ei ole määritelty, ja jättämään sitten funktion näissä kohdissa piirtämättä. Koko komento on tässä tapauksessa vaikkapa:

plot(g(x), x=-10..10, y=-5..5, discont=true);

Voit kokeilla, miltä kuvaaja näyttäisi ilman "y=-5..5"-termiä. Y-akselin säätely voi olla hyödyllistä, kun halutaan saada tarkka kuva jonkin funktion kulusta, vaikka kone usein skaalaakin akselin aika hyvin.

Kuvaajan kokoa voi säätää vetämällä hiirellä valkeista pikku neliöistä, jotka nkyvät kuvan ympärillä, kun hiiri viedään sen päälle. Huomaa, että Maple joutuu piirtämään kuvaajan numeerisesti, joten siinä "näkyviin" arvoihin ei voi eksaktissa tarkastelussa tietenkään luottaa. Kuten mikä tahansa komento, myös kuvaajan piirtäminen voidaan suorittaa uudestaan uusilla argumenteilla samassa kohtaa työtilaa siten, että argumentteja käydään muuttamassa ja painetaan taas ENTER.

Discont-termi on tämän funktion yhteydessä välttämätön, sillä kyseessä on rationaalifunktio, jonka määrittelyjoukko katkeaa tarkastelualueella. Kuvaajassa näkyy nyt yksi selkeästi määrittelyjoukkoon kuulumaton kohta. (Kokeile, mitä Maple piirtää, jos jätät Discont-termin pois!) Ilmeisesti funktio ei ole määritelty nollassa (kokeile nimittäjän arvoa kun x=0), mutta kuvaajasta näkemämme kohta on jokin muu. Funktiolla on kaksi reaalista kohtaa, joissa se ei ole määritelty, x=0 ja x=1/3, mutta tätä ei voi päätellä suoraan kuvaajasta, sillä pisteeseen x=0 ei liity muuten erikoista käyttäytymistä. (Ts. funktio ei kasva ja/tai vähene rajatta sen ympärillä. Funktiolla on jopa raja-arvo ko. pisteessä!) Nimittäjän nollakohdat pitää funktioita tutkittaessa siis aina ratkaista, esim. Maplella. Näin:

solve(3*x^2-x=0, x);

Ratkaiseminen käsinkin on tässä tapauksessa helppoa.

Määritellään eksponenttifunktio e^x. Kuten sanottu, Neperin luvulle e ei ole Maplessa omaa merkintää, vaan se on eksponenttifunktion arvo kohdassa 1. Funktio on exp(eksponentti) ja e ilmaistaan Maplessa täten kirjoittamalla "exp(1)". Määritellään:

h := x -> exp(x);

Määritellään sitten toisenlainen eksponenttifunktio, jonka kantaluku on pienempi kuin 1.

i := x -> exp(-x);

Tämä funktio on sama kuin (1/e)^x, koska e^-x=e^-1*x=(e^-1)^x=(1/e)^x. Piirretään molemmat funktiot samaan kuvaan. Tämä tapahtuu antamalla plot-komennolle ensinmmäisenä terminä joukko funktioita aaltosulkeiden {} sisällä ja pilkuilla erotettuina.

plot ({h(x), i(x)}, x=-4..4);

Funktioiden nähdään kasvavan ja vähenevän nopeasti. Näillä funktioilla ei ole nollakohtia, vaan ne ovat aina aidosti positiivisia, minkä voi testata solve-komennolla (mitään ratkaisua ei pitäisi tulla). Eksponenttifunktiot mielivaltaisella kantaluvulla voi ilmaista yksinkertaisesti x -> a^x, missä a on kantaluku.

Määrätään ja piirretään vielä logaritmifunktio samaan kuvaan exp(x):n kanssa:

j := x - > log(x);

(Tämä oli siis luonnollinen logaritmi.)

plot({h(x), j(x)}, x=-4..4, y=-4..4);

Huomataan, että luonnollisen logaritmin kuvaaja on sama kuin e-kantaisen eksponenttifunktion peilattuna viiston suoran y=x suhteen. Näin onkin aina käänteisfunktioiden laita.

Lopuksi määrittelemme ja piirrämme vielä sinifunktion k(x)=3sin(3x).

k := x -> 3*sin(3*x);

plot (k(x), x=-10..10);

Muotoilemalla kuvaajaa hieman siitä saadaan tällainen:

Kuvaajasta nähdään likimäärin, että funktion arvojoukko on [-3,3]. Tämä voidaan helposti todeta funktiota tutkimalla. Funktion jakso on kolme kertaa normaalin sinifunktion jaksoa tiheämpi: nollasta 2π :hin (x-akselilla hieman kuuden jälkeen) näyttäisi mahtuvan kolme jaksoa.

Sinifunktion nollakohdat voi päätellä yhdestä Maplen antamasta ratkaisusta:

solve(k(x)=0, x);

Maplen saa myös näyttämään kaikki ratkaisut. Tätä varten pitää asettaa Maplen ympäristömuuttuja _EnvAllSolutions arvoon "true".

_EnvAllSolutions:=true;

Tämän jälkeen mennään uudelleen edelliselle solve-riville ja painetaan ENTER.

Koneen antama vastaus 1/6π+1/3π _Z1~ tarkoittaa, että ratkaisut ovat 1/6π + vakio * 1/3π, missä vakio on kokonaisluku (siitä kirjain Z). Alaviiva osoittaa, että kyseessä on Maplen muodostama vapaavalintainen vakio, ykkönen Z:n perässä taas kertoo, että kyseessä oli ensimmäinen tällä laskentaistunnolla käyttöön otettu tämäntyyppinen vakio ja aaltoviiva kertoo, että vakio ei voi olla mitä tahansa (tässä tapauksessa sen on oltava kokonaisluku).

Harjoitus 3. Määrittele ja piirrä funktiot f(x)=x^15, g(x)=x^3-2*x^2+x, h(x)=x^3-2*x^2+x+0.01, i(x)=-(3x^2+2x)/(2x^2+3x), j(x)=e^(x^2) ja k(x)=tan(x). Ota piirtäessäsi huomioon mahdolliset määrittelyjoukon katkeamiset ja etsi järkevä skaalaus. Mitä voit kuvaajien perusteella sanoa funktioiden nollakohdista ja määrittelystä? Etsi g:n, h:n ja k:n kaikki nollakohdat (lukuunottamatta kompleksisia) ja määritä i:n määrittelyjoukko.

Maple laskee funktion tai lausekkeen raja-arvon limit-komennolla. Komennon jälkeen kirjoitetaan sulkeisiin ensin lauseke (joka voi siis olla myös funktion arvo jollain muuttujalla, esim. "f(x)") ja sitten muuttuja, jonka arvolla raja-arvoa etsitään, yhtäläisyysmerkki ja raja-arvon etsimispiste. Etsitään funktion f(x)=x^2 raja-arvo kohdassa 3.

limit (x^2, x=3);

Nähdään, että tässä tapauksessa raja-arvo on sama kuin funktion arvo. Rationaalifunktion raja-arvo määrittelyjoukon ulkopuolisessa pisteessä saattaa olla olemassa. Näin on yleensä asian laita, jos kuvaajasta katsoen funktio näyttäisi jatkuvan pisteen yli. Määritellään

f:=x->(5*x^2+2*x)/(3*x^2-x);

ja lasketaan

limit (f(x), x=0);

Tulokseksi saadaan -2, kuten kuvaajakin antaa ymmärtää. Joskus raja-arvo voi olla ääretön.

limit (abs(1/x), x=0);

Halutessasi voit piirtää tästä kuvaajan! Funktion arvot kasvavat rajatta kummaltakin puolelta, kun x lähestyy nollaa.

Raja-arvoa voi myös tutkia äärettömyydessä asettamalla x=infinity tai x= -infinity (negatiivinen äärettömyys). Monet funktiot kasvavat tai vähenevät rajatta tällaisessa tarkastelussa, mutta esim.

limit (f(x), x=infinity);

ja

limit (f(x), x=-infinity);

antavat molemmat tuloksen 5/3.

Aina raja-arvo ei ole määritelty. Lasketaan esim.

limit (1/x, x=0);

Kone vastaa "undefined", määrittelemätön, sillä funktion arvot vähenevät rajatta lähestyttäessä toiselta puolen pistettä x=0 ja kasvavat rajatta lähestyttäessä toiselta puolen.

Tutkimme vielä tapausta, jossa raja-arvo kertoo meille kahden funktion suhteesta. Laskemme raja-arvon lim_{x → ∞} (P(x)/e^x), missä P(x) on polynomifunktio, jollakin P(x):llä. Valitaan P(x)=x^3.

limit(x^3/exp(x), x=infinity);

Kone saa vastaukseksi 0. Vaihdellaan x^3:n paikalle eri polynomifunktioita ja huomataan, että tulos on aina sama. Tämä johtuu siitä, että eksponenttifunktio kasvaa lopulta aina mitä tahansa polynomifunktiota nopeammin, kun siirrytään eteenpäin x-akselilla, ja eksponentiaalifunktion arvot tulevat mielivaltaisen moninkertaisiksi vastaaviin polynomifunktion arvoihin nähden, kun x:ää kasvatetaan. Siksi tällaisen osamäärän raja-arvo äärettömyydessä on 0.

Harjoitus 4. Etsi rationaalifunktion f(x)=(x^3-2x^2)/(4x^3+x^2) määrittelyjoukosta puuttuvat pisteet ja laske funktion raja-arvo niissä, jos se löytyy.

Harjoitus 5. Ota selvää, miten edellisen tehtävän funktio sekä funktio g(x)=e^x käyttäytyvät äärettömyydessä ja miinus äärettömyydessä. Entä mikä on logaritmifunktion raja-arvo nollassa? Mieti ensin ja laske sitten Maplella.

Harjoitus 6. Mitkä ovat tangenttifunktion raja-arvot pisteessä π/2 ja äärettömyydessä? Onko niitä? Miksei?

Derivointi

Maple derivoi ja integroi symbolisesti määritelmien avulla. Varsinkin integraalifunktioiden ratkaisemiseen Maple on erittäin tehokas työkalu ihmisaivoihin verrattuna. Maplen derivaattaoperaatio diff suoritetaan aina lausekkeelle (funktio ja sen muuttuja suluissa) ja se palauttaa arvona lausekkeen. Maplessa on myös toinen derivaattaoperaattori D, jota emme tällä kurssilla tarvitse. Tämä operaattori käsittelee suoraan funktioita.

Derivointi kirjoitetaan muodossa diff(lauseke, muuttuja). Muuttuja on se muuttuja, jonka suhteen derivoidaan, kurssillamme siis funktion ainoa muuttuja. Derivoimme seuraavaksi polynomifunktion.

f := x -> x^3+3*x^2+4*x+1;

diff (f(x), x);

Kone antaa vastaukseksi funktion derivaatan 3x^2+6x+4. Voimme tarkistaa tuloksen laskemalla erotusosamäärän raja-arvon.

limit ((f(x+h)-f(x))/h, h=0);

Tutkitaan nyt kuvasta derivaatan suhdetta alkuperäiseen funktioon. Valitaan funktioksi f(x)=x^2 ja piirretään kuvaan sen ensimmäinen ja toinen derivaatta. Toinen derivaatta voidaan ilmaista Maplelle kahdella tavalla: diff(f(x), x, x) (derivoidaan kaksi kertaa x:n suhteen) tai diff(f(x), x$2) (lyhennysmerkintä).

f := x -> x^2;

plot({f(x), diff(f(x), x), diff(f(x), x$2)}, x=-4..4);

Ensimmäinen derivaatta näkyy tässä keltaisena viivana ja toinen punaisena. Kuvio havainnollistaa sitä, että derivaatta kuvaa funktiolle piirretyn tangentin kulmakerrointa. Kun liikutaan f(x):ää pitkin vasemmalta oikealle, sen jyrkkyys (eli kulmakerroin) kasvaa tasaisesti (kun oletamme, että laskevan funktion jyrkkyys on negatiivinen). Niinpä derivaatan kuvaaja on tässä tapauksessa nouseva suora.

Funktion toinen derivaatta on taas tämän nousevan suoran derivaatta. Sen jyrkkyys on kaikkialla sama (kulmakerroin 2), joten f(x):n toinen derivaatta on vakiofunktio 2. Kolmas derivaatta olisi kaikkialla 0, ja itse asiassa minkä tahansa polynomifunktion n+1:s derivaatta (missä n on polynomin aste) on kaikkialla 0.

Funktion derivaatta ei ole välttämättä kaikkialla määritelty. Esim. funktiolla g(x)=1/x ei ole derivaattaa kohdassa 0, koska koko funktiota ei ole siinä määritelty. Tämä voidaan todeta derivoimalla ja sijoittamalla derivaattaan x=0.

g := x -> 1/x;

diff(g(x), x);

Derivaatta ei saa arvoa, jos vastaukseen (-1/x^2) sijoitetaan x=0.

Derivaatan nollakohtien ratkaiseminen on hyödyllistä monissa matemaattisissa ongelmissa, kun etsitään funktion ääriarvoja jollakin välillä. Käytännössä tämä onnistuu solve-komennolla. Jos funktio on vaikkapa f(x)=x^3-2x, saadaan sen derivaatan nollakohdat näin:

f := x -> x^3-2*x;

solve(diff(f(x), x)=0, x);

Näin saaduista nollakohdista on sitten valittava se, joka tehtävän tarkasteluvälille osuu. Trigonometristen funktioiden tapauksessa Maple antaa taas vain yhden ratkaisun, ellei _EnvAllSolutions-muuttujaa ole ensin määritelty arvolle "true". Muut ratkaisut voi laskea käsin tai Maplella muuttujan arvon asettamisen jälkeen.

f := x -> sin(2*x);

_EnvAllSolutions := true;

solve(diff(f(x), x)=0, x);

Maplessa voi ratkaista differentiaaliyhtälöitä dsolve-komennolla. Komentoa käytetään samalla tavoin kuin tavallista solveakin, ratkaistavana on nyt vain funktio. Ratkaisemme aluksi differentiaaliyhtälön yy'=3x^2. Tämä on separoituva differentiaaliyhtälö, jonka ratkaisu on y=sqrt(2x^3+C), missä C on vakio.

dsolve (y(x)*diff(y(x), x)=3*x^2, y(x));

Huomaa, että koneelle on kirjoitettava jokainen funktio suluissa olevine muuttujineen ja derivaatat derivoimiskomennon avulla. Maple ei tunnista merkintää y'.

Maple sieventää vastausta siten, että ilmoitettu ratkaisussa esiintyvä vakio ei ole välttämättä integroimisvaiheessa saatu integroimisvakio, vaan jokin siitä ratkaistessa syntynyt toinen vakio (kuten tehdään myös oppimateriaalin kinkkutehtävässä: e^C on uusi vakio, koska e ja C ovat molemmat joitain vakioita). Tällä ei ole merkitystä, sillä vakio on kuitenkin vapaavalintainen, ellei alkuarvoehtoa ole annettu.

Voimme yrittää ratkaista Maplella kuinka vaikeita differentiaaliyhtälöitä tahansa. Käytännössä lineaarisia monimutakaisemmat differentiaaliyhtälöt eivät usein ratkea Maplenkaan voimin. Kokeile esim. yhtälön y''y'=sqrt(y)x ratkaisemista... Sen sijaan alkuarvotehtävien ratkaiseminen Maplella käy helposti. Ratkaisemme alkuarvotehtävän y'=y, y(0)=1 (tämä on materiaalissakin esiintyvä e^x:n määritelmä).

dsolve ({diff(y(x), x)=y(x), y(0)=1}, y(x));

Koneen pitäisi antaa vastaukseksi y(x)=e^x. Tämä on ainoa funktio, joka on itse oma n:s derivaattansa mielivaltaisella n. Yhtälö ja alkuarvo ryhmitellään dsolve-komennossa siis omaksi ryhmäkseen aaltosulkeiden sisään, kuten yo. kaavassa on tehty.

Toinen esimerkki alkuarvotehtävästä on materiaalin "kinkkutehtävä". Siinä lämpötilaa T kuvaa differentiaaliyhtälö T'=k(200-T), missä T on t:n eli ajan funktio ja k tuntematon vakiokerroin (tässä verrannollisuuskerroin). Alkuarvoehto oli tässä tapauksessa T(0)=21.

dsolve ({diff(T(t), t)=k*(200-T(t)), T(0)=21}, T(t));

Tämä ratkaisee kinkun lämpötilaa kuvaavan funktion lukuunottamatta k:n arvoa, jota ei näillä ehdoilla voidakaan saada selville. Huomaa, että ratkaisussa kerroin e^C on muutettu pelkäksi vakioksi edellä kuvatulla tavalla.

Harjoitus 10. Ratkaise differentiaaliyhtälö y'=(x+2)/(2y-1) käsin ja koneella. Ratkaise se sitten alkuarvolla y(0)=3 käsin ja koneella.

Harjoitus 11. Ns. Mooren lain mukaan tietokoneiden laskentakapasiteetin kasvu on suoraan verrannollinen kulloisenkin ajanhetken laskentakapasiteettiin. Ratkaise kulloistenkin tietokoneiden maksimikapasiteettia kuvaava indeksiluku i(t) ajan funktiona, kun maksimikapasiteettia kuvaava indeksiluku oli vuonna 2000 i(t)=100 ja vuonna 2002 i(t)=200. (Vinkki: käytä ensimmäistä alkuarvoa dsolve-komennossa integroimisvakion ratkaisemiseen ja toista sen jälkeen verrannollisuuskertoimeen.)

Yhtälöryhmän ratkaiseminen Maplella on yksinkertaista. Maplen solve-komennolla voidaan ratkaista useampia yhtälöitä yhtä aikaa. Tällöin yhtälöt on kirjoitettava aaltosulkeiden { } sisään. Esimerkiksi komento

solve({2*x+3*y-z=2, 3*x-2*y+2*z=-1, x-y+4*z=0});

                    /    7       29      1 \
                   { z = --, y = --, x = -- }
                    \    41      41      41/

Jos yhtälöryhmän informaatio ei riitä kaikkien tuntemattomien selvittämiseen, ratkaisuun jää ns. vapaita muuttujia. Maplen ratkaisussa näitä merkitään x=x. Vapaan muuttujan arvoksi käy mikä tahansa. Muiden muuttujien arvot riippuvat vapaiden muuttujien arvoista. Esimerkiksi:

solve({x+y-z=1, 2*x-2*y+z=2});

                 /    4            1         \
                { z = - y, x = 1 + - y, y = y }
                 \    3            3         /

Jos yhtälöryhmälle ei löydy lainkaan ratkaisua, Maple ei ilmoita tästä mitenkään, vaan siirtyy suoraan seuraavalle riville. Esimerkiksi seuraava syöte ei tuota mitään tulosta:

solve({x-y=0, x-y=2});

Maple osaa ratkaista yhtälöryhmän myös symbolisesti. Oletetaan, että haluamme ratkaista seuraavanlaisen yhtälöryhmän:

ax+by = 1
ax-by = 3,

solve({a*x+b*y=1, a*x-b*y=3}, {x, y});

                        /      1      2\
                       { y = - -, x = - }
                        \      b      a/

Harjoitus 12. Ratkaise Maplella kolmen tuntemattoman yhtälöryhmä

 -x +3y-4z = 1
 2x +4y +z = 2
-4x +cy-8z = 0.

Ennen kuin ryhdymme käsittelemään matriiseja ja vektoreita Maplen avulla, annetaan ensin komento

> with(LinearAlgebra);

Huom. Komentopakkaus LinearAlgebra on monipuolisempi ja tehokkaampi kuin vanha pakkaus linalg. Uutta pakkausta käytettäessä kaikki komennot (kuten Matrix, Vector jne.) on kirjoitettava isolla alkukirjaimella. Muuten Maple yrittää käyttää vanhan pakkauksen komentoja, mitkä eivät ehkä ole käyttötavaltaan aivan samanlaisia.

Matriisit

Matriisi syötetään Maplessa konstruktorin Matrix avulla. Tälle voidaan antaa matriisin alkiot hakasulkujen [ ] sisällä pilkuilla erotettuina, niin että jokainen rivi on vielä omien hakasulkujensa sisällä. Sijoitetaan esimerkiksi muuttujaan A eräs matriisi:

A := Matrix([ [1, 2], [3, 4], [5, 6] ]);

                               |1  2|
                          A := |3  4|
                               |5  6|

B := Matrix([ [18, 2], [-1, -3] ]);

                              |18   2|
                         B := |-1  -3|

Matriisin alkioihin viitataan kirjoittamalla hakasulkeet matriisin nimen perään. Voimme esimerkiksi katsoa, mikä on matriisin B ensimmäinen alkio kirjoittamalla B[1, 1]. Tulokseksi tulee 18. Lisäksi voimme vaikka sijoittaa tuon alkion paikalle uuden alkion:

B[1, 1] := 1;

                          B_1,1 := 1

Matriisitulon operaattorina toimii tavallinen piste. Esimerkiksi A:n ja B:n kertominen antaa tulokseksi

A.B;

                            |-1  -4|
                            |-1  -6|
                            |-1  -8|

Sijoitetaan vielä muuttujaan C eräs matriisi, jotta voimme kokeilla muitakin laskutoimituksia:

C := Matrix([ [3, 4], [-2, 1] ]);

                               | 3  4|
                          C := |-2  1|

2*(B+C);

                            | 8  12|
                            |-6  -4|

Käänteismatriisi saadaan komennolla MatrixInverse. Lasketaan esimerkiksi C:n käänteismatriisi:

MatrixInverse(C);
                           |1/11   -4/11|
                           |            |
                           |2/11   3/11 |

Error, (in LinearAlgebra:-LA_Main:-MatrixInverse) singular matrix.

Harjoitus 13. Ratkaise edellisen tehtävän yhtälöryhmä käänteismatriisin avulla.