Ensimmäinen tehtävä: Likimääräisen kuvaajan piirtäminen
Opettelemme laskemisen lisäksi piirtämään Excelillä kuvaajia annetusta datasta. Tätä ominaisuutta tarvitsemme mm. tilastollisissa menetelmissä, joita opiskellaan kurssin loppupuolella. Samalla hahmottelemme funktioiden kuvaajia arvopisteiden avulla. Tämä on periaatteessa sama menetelmä, jolla kuvaajia muodostetaan käsin: lasketaan funktion arvoja erilaisilla lähtöarvoilla ja piirretään arvopisteiden avulla likimääräinen kuvaaja.
Piirretään ensin funktion f(x)=(x^3)/2 (eli 1/2(x^3)) kuvaaja. Tätä varten lasketaan funktion arvoja sillä alueella, jolla kuvaajaa halutaan tutkia. Valitsemme nyt alueeksi välin [-6, 6]. Emme kuitenkaan voi laskea funktion kaikkia arvoja ko. välillä - niitähän on äärettömän paljon. Mikäli arvoja lasketaan riittävän tiheästi, saadaan kuitenkin funktion kuvajalle riittävän tarkka approksimaatio (tarkoituksesta riippuen). Kokeillaan arvojen laskemista 0,5:n välein, siis pisteissä -6; -5,5; -5; -4,5... ja sijoitetaan sitten pisteet kuvaajaan.
Aluksi tarvitsemme Excel-taulukon, jossa näkyvät funktion lähtöarvot ja arvot vierekkäisissä sarakkeissa. Funktion arvoja ei tarvitse laskea käsin, vaan ne saadaan Excelillä vaikkapa seuraavasti: Sijoitetaan ensin numerot -6 ja -5,5 valituista lähtöarvoista A-sarakkeeseen siten, että ruudussa A1 on luku -6 ja ruudussa A2 luku -5,5. Loput luvut sarakkeeseen saadaan maalaamalla eli valitsemalla aluksi ruudut A1 ja A2 vetämällä hiiren valkea ristiosoitin ruutujen päältä vasen nappi pohjassa ja jatkamalla sitten sarjaa vetämällä valitun alueen oikeasta alanurkasta alaspäin mustalla ristiosoittimella riittävän pitkälle.
Kirjoitetaan nyt soluun B1 kaava, joka antaa funktion arvon viereisessä solussa olevalla lähtöarvolla eli "=(A1^3)/2". Muista painaa ENTER kirjoitettuasi kaavan. Jos painat hiirellä jotain solua kaavaa kirjoittaessasi, Excel kirjoittaa automaattisesti tämän solun nimen siihen kohtaan kavaa, jossa olet! Tämä on syytä ottaa huomioon. Solun nimen saat kaavaan kuitenkin myös käsin kirjoittamalla.
Kaava on muuten sama kuin funktion lauseke, mutta alkuun ei tarvita f(x):ää (eli funktion nimeä) ja muuttujan paikalle kirjoitetaan ruutu, jossa muuttuja sijaitsee. Painettuasi ENTER ruudussa B1 pitäisi lukea funktion arvo -108. Kaava on kuitenkin edelleen ruudussa, minkä näet solun valitessasi ruudun yläosassa työkalurivien alla sijaitsevalla funktiorivillä (symboli "fx") tai kaksoisklikkaamalla solua.
Kun kaava on valmis, voit tarttua kaavasolua niinikään oikeasta alakulmasta mustalla ristiosoittimella ja vetää alaspäin. Tämä täyttää alkuarvojen viereiseen sarakkeeseen funktion kaavat (ja niiden tuloksina arvot). Tutkimalla kopioituja kaavoja B-sarakkeessa huomaat, että kopioidessaan kaavaa alaspäin Excel on myös sijoittanut joka kaavaan arvoruuduksi vastaavan viereisen sarakkeen ruudun; B2:ssa arvoruutu on siis A2, B3:ssa A3, B4:ssä A4 jne. Jos jossain sovelluksessa et halua Excelin muuttavan kaavaa vetämällä kopioitaessa vastaamaan uuden ruudun sijaintia, on solun nimi ilmaistava kaavassa muodossa "$A$1", missä "A":n paikalle tulee solun kirjain ja ykkösen paikalle numero. Dollarimerkki ($) kiinnittää sen koordinaatin, jonka edessä se on solun nimessä siten, että siirrettäessä tai kopioitaessa ko. koordinaatti ei muutu kaavan uutta sijaintia vastaavaksi.
kahden ensimmäisen sarakkeen pitäisi nyt näyttää tältä:
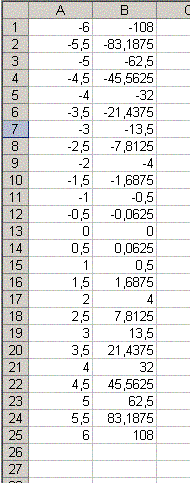
Jos olisimme hahmottelemassa kuvaajaa käsin, laskisimme vähemmän arvopisteitä ja pyrkisimme löytämään funktion kulun kannalta olennaisia pisteitä (esim. jos funktio saa hyvin lähellä toisiaan olevia arvoja, kannattaa kokeilla kauempana olevilla lähtöarvoilla). Excelillä voimme kuitenkin laskea vaivattomasti hyvinkin paljon pisteitä. Jotain rajaa kannattaa silti tässäkin tapauksessa pitää: Hyvin suuren aineiston piirtäminen kuvaajaan on joillakin laitteistoilla hidasta ja sitäpaitsi taulukkoa voi joutua selailemaan hankalasti ylös ja alas.
Piirrämme kuvaajan Excelin graafityökalulla, joka löytyy päätyökalurivin loppuvaiheilta. Valitse ensin hiirellä koko luomasi taulukko ja paina sitten graafityökalua:

Esiin tulee ikkuna "Chart Wizard - Step 1 of 4 - Chat Type", jossa on valittavana kaksi välilehteä. Pysymme "Standard Types" -välilehdessä ja valitsemme vasemmanpuoleisesta valikosta vaihtoehdon "XY (Scatter)". Tämä valinta tuottaa pistediagrammin, jossa vasen sarake tulkitaan automaattisesti x-akselin arvoiksi ja oikea sarake y-akselin arvoiksi. Pisteet voi myös yhdistää viivoilla, mikä tehdään valitsemalla oikeanpuoleisesta "kuvavalikosta" keskimmäisen rivin vasemmanpuoleinen tyyppi:
Sitten siirrytään kaavion luonnin seuraavaan vaiheeseen painamalla hiirellä "Next >" -nappia. Huomaa, että muita kaaviotyyppejä käyttäessäsi Excel käyttää kullekin kaaviotyypille sisäänrakennettuja oletuksia. Esim. nyt tehtävän kaavion pystyisi toteuttamaan myös viivadiagrammitoiminnolla, mutta valintoja pitäisi tehdä kaaviota luodessa enemmän - Excel olettaa viivadiagrammia tehdessään, että x-akselilla ei ole mitään erityisiä arvoja, vaan peräkkäiset ruudut tulevat "peräkkäisiin kohtiin" x-akselilla. Tämän pystyy muuttamaan, mutta se vaatii hieman lisäpuuhaa. Samaten muita diagrammityyppejä, esim. kakkudiagrammia tai ensimmäisen ikkunan toisesta välilehdestä löytyviä "mukautettuja tyylejä" koskevat omat alkuoletuksensa, joita sitten ehkä joutuu kiertämään, mikäli aineisto ei ole juuri ko. oletuksille soveltuva. Kannattaa kokeilla eri kaaviotyyppejä ja valintoja eri vaiheissa kaavion luontia ja miettiä sitten, millä logiikalla Excel minkäkinlaisen kaavion annetuista arvoista loi!
Seuraavan vaiheen voimme sivuuttaa painamalla uudestaan "Next >" -nappia. Tässä vaiheessa oltaisiin korjattu Excelin virheelliset tulkinnat taulukon arvojen merkityksistä, jos oltaisiin valittu viivadiagrammitoiminto. Voit tässäkin vaiheessa kokeilla, miten eri valinnat kaavioon vaikuttavat; apuna on ikkunassa näkyvä tulevan kaavion esikatselu.
Seuraavassa vaiheessa ikkunan otsikossa pitäisi lukea "step 3 of 4". Kirjoitamme (näkyvillä olevaan) "Titles"-välilehteen kaaviolle otsikon ja akseleille nimet. Kaavion otsikoksi voi laittaa vaikkapa "f(x)=(x^3)/2". Tämä kirjoitetaan kohtaan "Chart title:". Kahteen alempaan ruutuun kirjoitamme akselien nimet: x-akselille nimen "x" ja y-akselille "f(x)". Sitten valitsemme välilehden "Legend" ja otamme ruksin pois ruudusta "Show legend". Tällöin oikealla näkyvästä kaavion esikatselusta häviää funktion arvojen selite. Emme nyt tarvitse selitettä, koska meillä on vain yksi tutkittava arvosarja, jolla ei ole sen kummempaa nimeä. Selitettä voisi käyttää esim. useamman funktion tapauksessa.
Valitsemme vielä kerran "Next >". Prosessin viimeinen vaihe kysyy, upotetaanko kaavio muokattavaan taulukkosivuun vai tehdäänkö siitä oma sivunsa. Kätevyyssyistä valitsemme upotetun kaavion ("As object in:") ja painamme "Finish". Esiin tulee kaavio, jonka päällä on kaavion muokkaustyökalu:

Kaaviota voi siirtää vetämällä sen valkoisesta alueesta ja sen kokoa voi muokata tarttumalla ja vetämällä mustista neliöistä sen reunoilla. Näin hahmottelimme arvopisteiden avulla kysytyn funktion kuvaajan. Jos kuvaajasta ei tule jollakin funktiolla valaiseva, kannattaa kokeilla funktion arvojen laskemista tiheämmässä tai harvemmassa olevilla pisteillä eri puolilla määrittelyjoukkoa. Graafi päivittyy sitä mukaa kun sen arvoalue taulukossa muuttuu! Kokeile esim. mitä tapahtuu, jos muutat jonkin lähtöarvoista toiseksi, esim. -10:ksi.
Muunkinlainen kokeilu ja graafityökalun eri valintojen tutkiminen on tämän tehtävän yhteydessä suotavaa!
Harjoitus 3. Tee kuvaaja funktiosta f(x)=1/(x^2). Kuinka selkeä kuvaajasta tuli? Mitä kone piirtää funktion arvoksi pisteeseen 0, jos sitä yritetään piirtää? Onko tämä oikein? Mitä funktiolle tapahtuu tässä pisteessä?
Harjoitus 4. Yritä saada samaan kuvaan kuvaaja funktioista f(x)=x^2 ja g(x)=2. Miten tämä voisi onnistua? Miten saat kuvaajaan haluamiasi (x, y)-pisteitä, joita ei määrittele erityisesti mikään funktio?
Seuraavaksi tutustumme muutamaan numeeriseen menetelmään. Nämä menetelmät
on valittu pikemmin helposti ymmärrettävinä ja periaatetta opettavina
esimerkkeinä, niin Excelin käytön kuin matematiikankin kannalta
katsottuna, kuin käytännössä yleisimpinä menetelminä; käytännössä
esiintyvät numeeriset menetelmät ovat usein liian monimutkaisia tässä
selitettäviksi ja menetelmät vaihtelevat sovellusalueen mukaan.
Numeeristen menetelmien periaatteet ovat kuitenkin usein esimerkkiemme
kaltaisia.
Funktioiden ja yhtälöiden yhteydessä usein esiin tuleva tehtävä on
nollakohtien löytäminen. Aina se ei ole kuitenkaan analyyttisin menetelmin
mahdollista tai ainakaan helppoa. Esimerkiksi neljännen asteen polynomin
yleinen ratkaisukaava on niin pitkä, ettei sitä juurikaan käytetä, ja
viidennestä asteesta ylöspäin yleisiä ratkaisukaavoja ei ole olemassa.
Ensimmäinen menetelmä, johon tutustumme on ns. puolitus- eli
haarukointimenetelmä funktion nollakohtien löytämiseksi. Menetelmä
on logiikaltaan yksinkertainen ja selkeä. Nollakohtien ratkaisuun on
helppo käyttää numeerisia menetelmiä Excelissä, mikäli yhtälöitä
ratkaisevaa ohjelmaa, esim. Maplea ei ole käytössä.
Puolitusmenetelmän käyttöön vaaditaan eräitä esitietoja funktiosta, ja sen
avulla voidaan etsiä vain yhtä nollakohtaa kerrallaan. Ensinnäkin funktion
pitää olla määritelty välillä, jolla menetelmää käytetään, ja
lisäksi sen on oltava jatkuva kyseisellä välillä. Nollakohtia
löytyy vain, jos funktio vaihtaa merkkiä tutkittavalla välillä.
Itse asiassa puolitusmenetelmässä funktion on oltava eri merkkinen välin
alussa ja lopussa. Tällöinkin väliltä saattaa löytyä useita nollakohtia,
mutta menetelmällä niitä löytyy vain yksi. Parasta on valita väli, jolta
voimme olettaa löytävämme yhden nollakohdan, mikäli mahdollista.
Käytämme esimerkkinä puolitusmenetelmää funktion f(x)=x^3-2x erään
nollakohdan etsimiseen. Ensin valitsemme välin, jolta nollakohtaa
etsitään. Tämä tehdään arvaamalla. Jos käytettävissä tai tehtävissä on
luonnos kuvaajasta, sen avulla voidaan muodostaa varsin hyväkin arvaus.
(kuva funktiosta)
Etsimme nyt nollakohtaa funktiosta välillä [1, 2]. Tässä tapauksessa
näemme kuvaajasta, että nollakohta on jossakin tuolla välillä. Funktio on
tällä alueella kasvava, joten täyttäessään ehdot, joilla menetelmää voi
käyttää se saa negatiivisen arvon välin alkupisteessä ja positiivisen
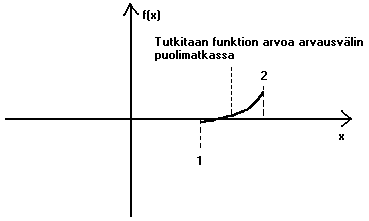
arvon loppupisteessä. Nyt puolitusmenetelmä toimii graafisesti näin:
Funktion arvoa tutkitaan valitun välin puolimatkassa. Mikäli ei käy niin
hyvin, että funktion nollakohta on juuri tässä pisteessä, valitaan
tarkasteltavaksi uusi, lyhyempi väli. Jos funktion arvo on
puolituspisteessä positiivinen (kuten esimerkissä), siirrytään
tarkastelemaan puolivälin alapuolista väliä (alkuperäisen välin
alkupisteessähän funktio oli negatiivinen, joten nollakohdan pitää löytyä
tältä väliltä) eli väliä [1, 1,5]. Jos funktion arvo puolituspisteessä tas
olisi positiivinen, valittaisiin seuraavaksi tarkasteluväliksi [1,5, 2].
Huomaa, että jos funktio olisi ollut alkuperäisen välin alussa
positiivinen ja lopussa negatiivinen, valinta tehtäisiin päinvastoin!
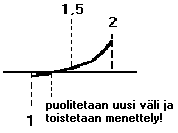
Seuraavaksi puolitetaan saatu uusi, lyhyempi väli ja lasketaan taas
funktion arvo puolituskohdassa. Kuvassamme funktio saa tässä kohdassa jos
hyvin lähellä nollaa olevan arvon. Toistetaan sama menettely kuin
edellisessä kohdassa: jos funktion arvo on uudessa, lyhyemmän välin
puolivälissä positiivinen, valitaan seuraavaksi tarkasteluväliksi tämän
välin alempi puolisko [1, 1,25], muussa tapauksessa ylempi puolisko [1,25,
1,5]. (Huomaa taas, että meneteltäisiin päinvastoin, jos alkuperäisen
välin päissä funktio olisi saanut erimerkkiset arvot kuin nyt!)
Tätä menetelmää toistamalla saadaan yhä lyhyempiä ja lyhyempiä valejä,
joiden sisään funktion eräs nollakohta jää. Toisaalta välin puolimatka
tarjoaa joka askeleella yhä tarkemman arvauksen nollakohdaksi. Excelissä
puolitusmenetelmä voidaan toteuttaa vaikkapa näin:
Ensin kirjoitetaan funktio muistiin, esim. soluun A1. Sitten tehdään neljä
saraketta: "välin alkupiste", "välin loppupiste", "puoliväli" ja
"f(puoliväli)" eli funktion arvo puolivälissä. Huomaa, että mikäli teksti
ei mahdu haluamaasi soluun, voit muuttaa sarakkeen kokoa vetämällä
sarakkeen koordinaattiruutujen (harmaat ruudut, joissa on sarakkeen nimi)
välistä mustalla kaksoisnuoliosoittimella. Tässä esimerkissä sarakkeiden
nimet ovat ruuduissa C1-F1.
Aluksi kirjoitamme ruutuihin C2 ja D2 alkuperäisen välin alku- ja
loppupisteet (siis tässä tapauksessa luvut 1 ja 2). Ruutuun E2 kirjoitamme
näiden pisteiden puolivälin kaavan "=(C2+D2)/2". (Älä siis kirjoita
lainausmerkkejä!) Kun kaava on valmis, ja painat ENTER, ruutuun pitäisi
tulla laskun tulos, tässä tapauksessa 1,5. Sitten tarvitsemme funktion
arvon puolivälipisteessä. Kirjoitamme ruutuun F2 kaavan, joka vastaa
funktion arvon laskemista äsken lasketussa pisteessä: "=E2^2-2*E2". Tämän
kaavan pitäisi antaa tulos 0,375. Nyt kaavion pitäisi näyttää
jotakuinkin tältä:
Ruutuihin C3 ja D3 tarvitaan nyt uuden välin alku- ja loppupisteet. Tähän
käytetään Exceliin sisäänrakennettua ehtolausetoimintoa. Uuden välin
alkupistehän on tässä tapauksessa edellisen välin puoliväli, jos
f(puoliväli) on negatiivinen (eli nollaa pienempi), muuten taas edellisen
välin alkupiste. Excelin ehtolause on muotoa "=IF(testi; arvo jos testi
onnistuu; arvo jos testi ei onnistu)". Tässä tapauksessa kirjoitamme
ruutuun C3 siis "=IF(F2<0; E2; C2)". Näin Excel valitsee uuden välin
alkupisteeksi edellisen puolivälin, jos arvo siinä on negatiivinen,
muutoin edellisen välin alun. Jos alun perin olisimme valinneet välin,
jolla funktion arvo on alussa positiivinen ja lopussa negatiivinen
(tämän voi tarkistaa laskemalla), kaava olisi muuten samanlainen, mutta
"<"-merkin tilalla olisi ">". Tämä johtuu siitä, että jouduttaisiin
valitsemaan uusi väli juuri päinvastoin. Tätä voit tutkia vaikkapa
piirtämällä itse kuvaajan päinvastaisesta tapauksesta.
Ruutuun D3 tarvitaan uuden välin loppupiste. Voidaan käyttää samaa kaavaa
kuin edellisessä ruudussa sillä erotuksella, että tulokseksi pitää saada
joko edellisen välin loppupiste tai puoliväli. Kaavaksi tulee siis
"=IF(F2<0; D2; E2)". Tässäkin kaavassa olisi ">"-merkki "<"-merkin
tilalla, jos alkuperäisen välin päätepisteiden merkit olisivat
olleet toisin päin. Näiden kaavojen sijoittamisen jälkeen kaavion pitäisi
näyttää tältä:
Nyt olemme kirjoittaneet kaikki tarpeelliset kaavat. Kone pitäisi vielä
saada suorittamaan samat toimenpiteet uuden välin rajojen avulla. Tämä
onnistuu Excelin kaavojen älykkäällä kopiointiominaisuudella. Valitaan
siis ruudut C3 ja D3, tartutaan oikean alakulman mustasta neliöstä ja
vedetään alaspäin. Kone täyttää taulukkoa kaavoja kopioimalla (siten, että
seuraavalla rivillä kaavat viittaavat aina riviä alempiin lähtösoluihin).
Aluksi tulevissa arvoissa ei ole järkeä. Siksi pitää kopioida myös solujen
E2 ja F2 kaavoja samalla tavalla alaspäin. Taulukosta tulee nyt jotenkin
tämän näköinen:
Nähdään, että välien puolivälit lähestyvät funktion nollakohtaa, sillä
funktion arvot lähenevät nollaa. Mitä pidemmälle kaavoja kopioidaan, sitä
tarkemmaksi arvio tulee. Mikäli et saa desimaaleja näkymään haluamallasi
tavalla, valitse koko taulukko ja paina sen päällä hiiren oikeaa
nappia. Valitse esiintulevasta valikosta "Format Cells..." ja muuta
siellä numeroiden esitystapaa. (tähän tulee vielä tarkempi kuvaus, minulla
on nyt käytössäni OpenOffice, joka saattaa tuossa poiketa hieman
Excelistä)
Puolitusmenetelmällä saadaan esim. kysytylle funktion nollakohdalle arvo
1,414, jos sitä kysyttäisiin kolmen desimaalin tarkkuudella.
Puolitusmenetelmä on numeerisista nollakohdanetsintämenetelmistä
ymmärrettävin, mutta myös yksi tehottomimpia: tulos tarkentuu melko
hitaasti. Seuraavaksi esittelemme parannetun ja tehokkaamman Newtonin
menetelmän. Puolitusmenetelmän ymmärtäminen on kuitenkin hyvä johdatus
numeeristen menetelmien maailmaan.
Harjoitus 5. Etsi samalla menetelmällä saman funktion toinen
nollakohta väliltä [-2, -1]. Pohdi, mitä joudut tekemään
merkinnöille ehtolausekkeissa ja miksi. Hahmottele sitten Excelillä
sinifunktion kuvaaja ja etsi puolitusmenetelmällä sen nollakohtia väleiltä
[2, 5] ja [1, 2]. Löytyikö nollakohtia? Mistä tiedät tämän? Mitä tapahtui
jälkimmäisellä välillä?
Tehokkaampi menetelmä nollakohtien etsimiseen on ns. Newtonin
menetelmä, joka perustuu funktion sivuajien eli tangenttien
ominaisuuksiin. (Älä sekoita tätä tangenttifunktioon, vaikka määritelmien
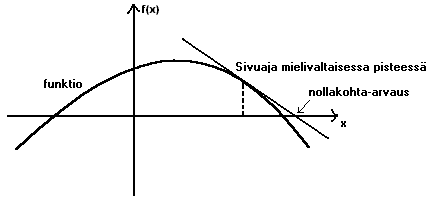
välillä onkin yhteys!) Graafisesti ottaen menetelmässä piirretään
funktiolle sivuaja johonkin pisteeseen ja muodostetaan nollakohta-arvaus
sen avulla. Arvaukseksi tulee sivuajan nollakohta.
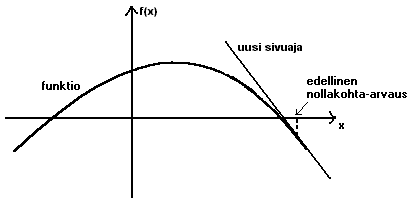
Sitten piirretään uusi sivuaja funktiolle saadussa arvauskohdassa, ja sen
nollakohdasta tulee uusi arvaus. Esimerkkikuvassamme tämä päätyy jo hyvin
lähelle funktion todellista nollakohtaa.
Menettelyä toistetaan kuten puolitusmenetelmässäkin. Erona on se, että
saatu arvaus lähestyy funktion nollakohtaa hyvin paljon nopeammin.
Karkeana arviona voidaan esittää, että oikeiden desimaalien määrä
arvauksessa yleensä suurin piirtein kaksinkertaistuu joka askeleella.
Newtonin menetelmän heikkous on, että se ei toimi aina, milloin
puolitusmenetelmä toimii. Toisaalta kaikkia puolitusmenetelmän esitietoja
ei tarvita (esim. ei ole mitään tarkasteluväliä, jonka eri päissä funktion
pitäisi saada erimerkkiset arvot). Mielivaltaisella reaaliarvoisella
funktiolla ei tietenkään aina edes ole nollakohtia, emmekä nyt käy läpi
ehtoja, joilla Newtonin menetelmä toimii. Meille riittää seuraava tieto:
jos Newtonin menetelmän antamat arvaukset lähestyvät jotain pistettä,
piste on tutkittavan funktion eräs nollakohta. Toisia nollakohtia voi
etsiä muuttamalla menetelmän lähtöpistettä. Hyviä lähtöpisteitä voi
löytää funktion kuvaajaa hahmottelemalla.
Käyttääksemme Newtonin menetelmää numeerisesti meidän on pystyttävä
muodostamaan funktiolle sivuajafunktio jossain pisteessä. Tämä
tehdään funktion derivaatan avulla.
Derivaatan arvo tietyssä pisteessä kuvaa funktion jyrkkyyttä ko.
pisteessä. Itse asiassa derivaatta on nimenomaan pisteeseen piirretyn
sivuajan kulmakerroin. Tämä tarkoittaa sitä, että sivuajafunktion
yhtälö on muotoa s(x)=kx+a, missä k on funktion f derivaatta ja a jokin
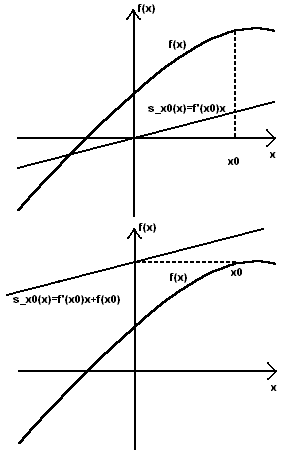
vakio. Pisteessä x0 sivuaja s_x0 on siis s_x0(x)=f'(x0)x+a. Meidän pitää
vielä ratkaista a.
Jos a olisi 0, s_x0:n kuvaaja kulkisi origon kautta. Siirrämme sitä ensin
y-akselia ja sitten x-akselia pitkin, niin että saamme lopulta tulokseksi
halutun sivuajan. Siirretään kuvaaja ensin kulkemaan arvolla x=0 siltä
korkeudelta, millä sen pitäisi kohdata alkuperäinen funktio eli siirretään
sitä y-akselia pitkin. Tämä tapahtuu lisäämällä a:han funktion arvo x0:ssa.
Nyt meillä on suora s_x0(x)=f'(x0)x+f(x0), siis sivuajan suuntainen suora,
jossa a:na on funktion arvo sivuamispisteessä. Pitäisi vielä siirtää
suoraa x-suunnassa siten, että se saisi pisteessä x0 sen arvon, jonka se
nyt saa nollassa. Korvataan nyt suoran kaavassa esiintyvä x lausekkeella
(x-x0), joka saa arvon 0, kun x=x0. Tällöin kuvaaja pysyy muuten samana,
mutta siirtyy x0:n verran, koska se saa samat arvot kuin edellinen versio
kohdissa, jotka ovat x0:n päässä edellisistä.
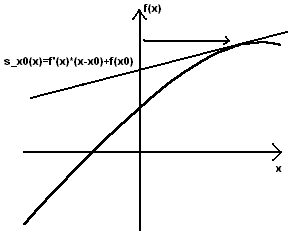
Sivuajan kohdassa x0 yhtälöksi saadaan siis s_x0(x)=f'(x0)*(x-x0)+f(x0),
auki kerrottuna s_x0(x)=f'(x0)x-f'(x0)x0+f(x0). Sivuajan nollakohdassa
s_x0(x) on nolla, joten se saadaan ratkaisemalla x yhtälöstä
f'(x0)x-f'(x0)x0+f(x0)=0. Tällöin sivuajan nollakohta on x=x0-f(x0)/f'(x0)
eli sivuajan piirtämispiste miinus funktion ja derivaatan arvojen erotus
ko. pisteessä.
Exceliin sijoitettuna Newtonin menetelmä on näin ollen hieman kevyempi
kuin sijoitusmenetelmä: ehtolauseita ei tarvita, ainoastaan alkuarvaus ja
sivuajan nollakohta arvauspisteessä. Askelta kohti suoritetaan
periaatteessa vain yksi toimenpide, mutta selvyyden vuoksi käytämme neljää
saraketta. Merkitään taas aluksi ruutuun A1 muistiin käsiteltävä funktio.
Olkoon se sama kuin edellisessä tehtävässä: f(x)=x^3-2x. Ruutuun C1
kirjoitetaan "arvauspiste", ruutuun D1 "f(arvauspiste)", ruutuun E1
"f'(arvauspiste)" ja ruutuun F1 "sivuajan nollakohta".
Ensimmäinen arvaus voisi olla vaikkapa 1. Kirjoitetaan tämä luku ruutuun
C2. Sitten kirjoitetaan funktion arvon laskeva kaava "=C2^3-2*C2" ruutuun
D2. Funktio on nyt derivoitava. Tulokseksi saadaan f'(x)=3x^2-2, joten
ruutuun E2 kirjoitetaan "=3*C2^2-2", derivaatan arvo arvauspisteessä.
Ruutuun F2 kirjoitetaan arvauspisteeseen piirretyn sivuajan nollakohta,
joka on äskeisen päättelyn nojalla "=C2-D2/E2". Tämä on itse asiassa
seuraava arvauspiste, joten ruutuun C3 kirjoitetaan yksinkertaisesti
"=F2". (Tehtävästä oltaisiin selvitty myös ilman F-saraketta
kirjoittamalla sivuajan nollakohdan kaava suoraan tähän ruutuun.) Nyt
taulukon pitäisi olla jokseenkin tällainen:
Jos saat soluihin eri lukuja kuin kuvassa, tarkista kaavasi! Menetelmä on
nyt valmiina; kopioimme taas kaavoja alaspäin. Kopioidaan ensin C3:a
valitsemalla ruutu ja vetämällä oikeasta alanurkasta, ja sitten valitaan
D2, E2 ja F2 ja kopioidaan niitä saman verran alaspäin. Asetetaan jälleen
riittävästi desimaaleja näkymään valitsemalla taulukko ja säätämällä
lukujen esitystapaa "Format Cells" -toiminnolla. Tulos on jotain tämän
näköistä (jos luvut esitetään kuuden desimaalin tarkkuudella):
Huomataan ensinnäkin, että menetelmä toimii tässä tapauksessa - arvot
suppenevat kohti nollakohtaa. Huomataan myös, että menetelmällä päästään
hyvin nopeasti hyvin lähelle nollakohtaa. Ei myöskään tarvitse miettiä,
suurempi- ja pienempikuin-merkkisääntöjä niin kuin puolitusmenetelmässä.
Siksipä Newtonin menetelmää kannattaa käyttää puolituksen sijasta, jos se
vain toimii.
Harjoitus 6. Etsi Newtonin menetelmällä kosinifunktion nollakohtia.
Käytä apuna Maplea ja piirrä kosinifunktion kuvaaja. Mistä alkupisteistä
lähtien löydät mitäkin nollakohtia? Pystytkö sanomaan jotain summittaista
sääntöä nollakohtien löytymiselle tässä tapauksessa?
Tutkimustehtävä (vapaaehtoinen lisätehtävä kiinnostuneille). Minkä
tyyppisissä tilanteissa Newtonin menetelmä ei toimi? Pohdi itse tai etsi
tietoa netistä. Vaikkapa tästä
voi aloittaa...
Numeerinen integrointi tarkoittaa määrätyn integraalin arvon
approksimoimista (eli arvioimista) menetelmin, jotka eivät vaadi
integraalifunktion muodostamista. Tämä on hyödyllistä, koska useiden
funktioiden integraalifunktiot ovat erittäin hankalia muodostaa ja
käsitellä, eikä niitä tämän kurssin tiedoilla voi saada selville.
Numeerisia integrointimenetelmiä on kehitetty lukuisia, mutta tutustumme
niistä nyt vain yhteen helppotajuisimmista, ns.
puolisuunnikassääntöön.
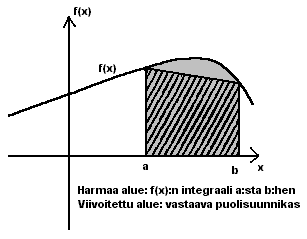
Määrätty integraali on (x-akselin yläpuolella) sama kuin funktion kuvaajan
ja x-akselin väliin jäävä ala integraalin rajojen sisällä. Kaikessa
yksinkertaisuudessaan puolisuunnikassääntö sanoo, että eräs approksimaatio
tälle alalle on sellaisen puolisuunnikkaan ala, jonka kulmat ovat
x-akselilla välin alku- ja loppupisteissä sekä funktion kuvaajalla välin
alku- ja loppupisteissä.
Puolisuunnikkaan ala on pohja (tässä a:sta b:hen) kertaa siihen suhteessa
suorassa kulmassa olevien sivujen pituuden keskiarvo, siis tässä
(b-a)*(f(a)+f(b))/2. Tämä ei ole kuitenkaan vielä kovin tarkka arvio
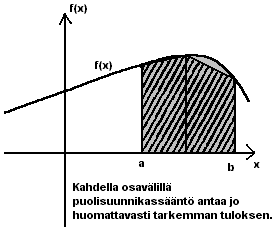
integraalille a:sta b:hen. Arviota voidaan tarkentaa jakamalla
integroimisväli kahteen osaväliin, soveltamalla näille väleille erikseen
puolisuunnikassääntöä ja laskemalla saadut pinta-alat yhteen. Merkitään
osavälin pituutta kirjaimella h. Tällöin h=(b-a)/2 ja puolisuunnikkaiden
yhteenlaskettu pinta-ala on h*(f(a)+f(a+h))/2+h*(f(a+h)+f(b))/2.
Integroimisväli voidaan edelleen jakaa useampiin osiin, jolloin h=(b-a)/m,
jos m on osavälien lukumäärä, ja yhteenlasketuksi pinta-alaksi saadaan
h*(f(a)+f(a+h))/2+h*(f(a+h)+f(a+2h))/2+h*(f(a+2h)+f(a+3h))/2+ ...
+h*(f(a+(m-1)h)+f(b))/2. Toteutamme tämän yhteenlaskun nyt Excelin avulla.
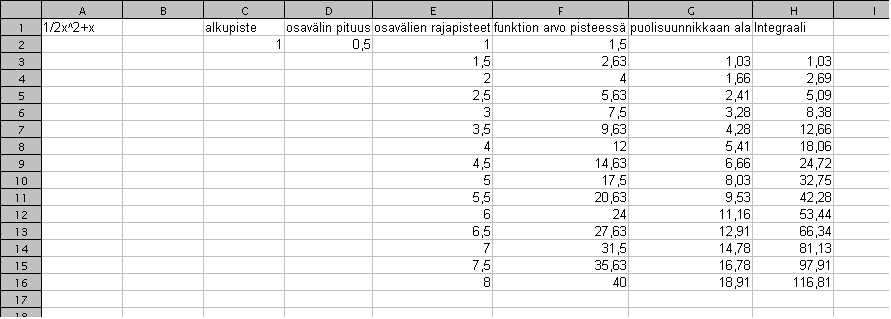
Integroidaan esimerkkinä numeerisesti funktiota f(x)=1/2x^2+x.
Kirjoitetaan funktion lauseke taas muistiin ruutuun A1. (Tämän
funktion integraalifunktiokin on kyllä aika helppo löytää. Mikä se on?)
Integroimisvälistä valitaan vain alkupiste; loppupiste voidaan vapaasti
valita kohta muodostettavasta taulukosta. Valitaan alkupisteeksi 1.
Ruutuun C1 voimme nyt kirjoittaa "alkupiste", ruutuun D1 "osavälin
pituus", ruutuun E1 "osavälien rajapisteet", ruutuun F1 "funktion arvo
pisteessä", ruutuun G1 "puolisuunnikkaan ala" ja ruutuun H1 "Integraali".
Tässä tarkastelussa määritämme käsin alkupisteen ja osavälin pituuden.
Olisi mahdollista laatia taulukko myös niin, että tarkasteluväli olisi
etukäteen määrätty ja osavälien määrä annettaisiin käsin.
Sijoitetaan ruutuun C2 alkupisteemme arvo 1 ja D2:een aluksi osavälin
pituudeksi 0,5. Ruutuun E2 sijoitamme ensimmäisen osavälin alkupisteen,
joka on sama kuin koko tarkastelualueen alkupiste, siis "=C2". Ruutuun E3
sijoitetaan edellinen arvo + osavälin pituus, siis "=E2+$D$2". Huomaa
dollarimerkit kaavassa! Ne takaavat, että osavälin pituus luetaan aina
samasta ruudusta huolimatta siitä, mihin tämän ruudun kaavaa
kopioidaan. Dollarimerkit siis estävät Exceliä muuttamasta kaavan
syöttöruutua "älykkäästi" kaavaa kopioitaessa. Ensimmäinen merkeistä
kiinnittää syöttöruudun sarakkeen ja toinen rivin.
Ruutuun F2 laskemme funktion arvon viereisen ruudun osoittamassa
pisteessä. Sijoitamme siis funktion lausekkeeseen viereisen ruudun nimen,
näin: "=0,5*E2^2+E2". (1/2=0,5)
Ruudun G2 jätämme tyhjäksi: mitään puolisuunnikasta ei ole vielä
muodostunut, koska on vasta yksi arvopiste. Kirjoitamme sarakkeen
ensimmäisen kaavan ruutuun G3. Tällä kaavalla kuvaamme sen
puolisuunnikkaan alaa, joka muodostuu ensimmäiselle osavälille.
Sijoittamalla alan kaavaan vastaavat arvoruudut saadaan kaava
"=$D$2*(F2+F3)/2". Tässä siis kerrotaan osavälin pituudella edellisen
osavälin funktion arvojen keskiarvo. Huomaa, että osavälin pituuden
sisältävä ruutu on taas kaavassa kiinnitettävä dollarimerkeillä!
Lopulta kirjoitamme ruutuihin H3 ja H4 tarvittavat kaavat numeerisen
integraalin laskemista varten. H3:ssa integraali on sama kuin ensimmäisen
puolisuunnikkan ala, siis "=G3". H4:ssä pitää edellinen arvo laskea yhteen
seuraavan puolisuunnikkaan alan kanssa. Se tulee ruutuun G4, joten kaava
"=H3+G4" kerryttää seuraavan puolisuunnikkaan alan jo laskettuun arvoon.
Taulukon pitäisi nyt olla tämän näköinen:
Taulukon arvot eivät ole vielä oikeat; osa kaavoista viittaa tyhjiin
ruutuihin, jotka täytetään vasta nyt kaavoja kopioimalla. Siispä
kopioidaan. Ensin merkataan solu E3 ja kopioidaan sitä alaspäin, sitten
F2:ta, sitten G3:a ja lopulta H4:ää. Otetaan esiin riittävän monta
desimaalia (tässä olen tyytynyt kahteen; arviot eivät kuitenkaan ole
älyttömän tarkkoja) ja saadaan lopullinen taulukko:
Nyt oikeanpuolimmaisesta sarakkeesta voi lukea numeerisen integraalin
1:stä mihin tahansa sarakkeen E pisteeseen. Taulukko muuttuu, jos vaihdat
ruutuihin C2 ja/tai D2 eri integroimisvälin alun ja osavälin leveyden.
Kokeile! Huomaa, että mitä lyhyempi osaväli on, sitä pidemmälle joudut
kopioimaan kaavoja saadaksesi selville integraalin johonkin asti.
Toisaalta arvo tarkentuu.
Tämä menetelmä antaa oikean integraalin myös tapauksessa, jossa funktio
saa negatiivisia arvoja, sillä "puolisuunnikkaan pystyreunalle" tulee
tällöin negatiivinen pituus, jolloin "pinta-alaksikin" voi tulla
negatiivinen luku. Jos siis integroit numeerisesti saadaksesi selville
käyrän ja x-akselin välisen pinta-alan, sinun on tätä menetelmää
käyttäessäsi muistettava tutkia erikseen integroimisvälin alueita, joilla
funktion arvo saa eri merkit ja summata negatiivisten integraalien
vastaluvut positiivisten kanssa!
Harjoitus 7. Integroi numeerisesti välillä [1, 3] funktio
exp(sqrt(x)), missä sqrt tarkoittaa neliöjuurta. Funktioiden exp ja sqrt
nimet ovat samat Excelissä. Muodosta integraali neljällä, kahdeksalla ja
32 osavälillä. Mitä huomaat integraalin tarkkuudesta? Yritä Maplella
muodostaa tehtävän funktiosta integraalifunktio. Miksi Numeerinen
integrointi on tässä hyödyllistä?
Harjoitus 8. Selvitä graafista integraalia apuna käyttäen ja
kokeilemalla, millä integroimisvälin alulla funktion f(x)=x^3-2x
integraaliksi saadaan 0, jos integroimisvälin loppu on a) 3, b) 5 tai c)
-3. C-kohdassa aseta osavälin pituudeksi negatiivinen luku! Mitä
havaitset? Onko tämä uskottavaa? Mitä se kertoo funktiosta? Miten
c-kohdassa integraalin arvo muodostui, kun integroitiin "takaperin"?
Tässä tutustumme pinnallisesti neljään tilastolliseen perustunnuslukuun,
opimme laskemaan ne Excelillä ja piirrämme lineaarisen ja
eksponentiaalisen regressiokuvaajan.
Ensimmäinen tunnuslukumme on keskiarvo. Tämä luku soveltuu
tilastollisille aineistoille, joiden yksittäiset alkiot ovat numeroarvoja.
Keskiarvo lasketaan kaavalla Σ(xi)/n, missä
xi:t ovat tilastollisen aineiston yksittäiset arvot ja n
arvojen määrä. Iso sigma kuvaa summaa, ja sanallisesti keskiarvon voikin
ilmaista aineiston arvojen summana jaettuna arvojen määrällä.
Esim. tulojakaumassa keskiarvo kertoo, kuinka paljon rahaa aineiston
ihmisillä olisi henkilöä kohti, jos rahat jaettaisiin tasan. Keskiarvo on
matemaattisesti helppokäyttöinen ja ominaisuuksiltaan selkeä tunnusluku,
jota käytetään melkein kaikessa tilastollisessa laskennassa (esim.
kahta tai useampaa eri aineistoa verrattaessa). Periaatteessa samalla
kaavalla lasketaan tilastosta myös ns. odotusarvo, jolla kuvataan
keskimääräistä odotettavissa olevaa uutta arvoa, jos tilasto käsitetään
jonkin satunnaismuuttujan ilmenemäksi.
Keskiarvo on kuitenkin leimallisesti koko aineiston abstrakti
ominaisuus. Sillä saattaa olla aineiston esitystavasta riippuen hyvinkin
heikko kyky kuvailla aineistoa. Esim. jakaumassa, jossa hyvin pieniä ja
hyvin suuria arvoja on paljon, mutta keskisuuria ei lainkaan, yksikään
aineiston arvo ei muistuta läheskään keskiarvoa. Keskiarvo kuvaa
aineistoa parhaiten, jos aineiston jakauma on symmetrinen ja kasautunut
keskiarvon lähistölle kuten esim. normaalijakauma.
Keskiarvo lasketaan Excelissä funktiolla AVERAGE. Syötämme ruutuihin
A1-A10 nyt seuraavan aineiston:
Sitten kirjoitamme ruutuun C1 aineiston keskiarvon kaavan:
"=AVERAGE(A1:A10)". Kaksoispiste tarkoittaa kaikkia ruutuja, jotka jäävät
alku- ja loppuruudun väliin. (Esim. A1:B10 tarkoittaisi ruutuja A1:stä
A10:een ja ruutuja B1:stä B10:een!) Ruutuun pitäisi tulla keskiarvo
4,9.
Seuraavaksi laskemme aineiston moodin eli tyyppiarvon. Moodi on se arvo,
joka esiintyy aineistossa useimmin. Moodi soveltuu myös sellaisten
aineistojen kuvailuun, joissa arvot eivät ole numeerisia. Esim.
suomalaisten siviilisäätymoodi on se siviilisääty, johon suurin osa
suomalaisista kuuluu. Moodi voi poiketa keskiarvosta hyvinkin paljon, ja
se kuvaa aineistoa usein hyvin tilanteissa, joissa hyvin suuressa
aineistossa arvot selkeästi keräytyvät tiettyihin kohtiin. Lasketaan
ruutuun C2 aineistomme moodi kaavalla "=MODE(A1:A10)". Tuloksen pitäisi
olla 3.
Mediaani on kolmas havainnollinen aineiston "keskiluku", joka kertoo,
minkä arvon ala- ja yläpuolella on yhtä monta aineiston arvoa.
Mediaani siis jakaa aineiston keskeltä kahtia. Mikäli aineiston arvojen
lukumäärä on parillinen, mediaani on kahden keskimmäisen luvun keskiarvo
(siis kun aineisto on ensin järjestetty suuruusjärjestykseen). Mediaani
kertoo esim. tulojakaumasta usein enemmän kuin keskiarvo, sillä keskiarvoa
saattavat painaa kovinkin ylös yksittäiset hyvin suuret arvot muuten
pieniarvoisessa aineistossa. Tavallaan mediaani tällöin kertoo, millainen
on "keskiverto" tulonsaaja. Laskemme aineistomme mediaanin kaavalla
"=MEDIAN(A1:A10)" ruutuun C3. Tulos: 4,5.
Neljäs ja viimeinen tunnuslukumme ei ole "keskiluku", kuten muut kolme,
vaan ns. hajontaluku, joka kertoo, kuinka paljon aineiston arvot
poikkeavat keskiarvosta. Hajontalukuja voi laskea useilla tavoilla, mutta
matemaattisesti käyttökelpoisin on ns. keskihajonta (standard
deviation), jota toisinaan myös kutsutaan keskivirheeksi tai
keskipoikkeamaksi (näitä termejä käytetään kuitenkin joskus ristiin muiden
käsitteiden kanssa, joten keskihajonta lienee varmin tapa puhua ko.
luvusta). Keskihajonta lasketaan korottamalla jokaisen arvon ja aineiston
keskiarvon erotus neliöön, summaamalla nämä neliöt, jakamalla aineiston
määrällä vähennettynä yhdellä ja ottamalla koko jutusta neliöjuuri.
Menettely muodostaa luvun, joka kuvaa aineiston arvojen poikkeamaa
keskiarvosta, mutta käyttää siihen normaalista summaamisesta poikkeavaa
ns. 2. normin mukaista menettelyä, joka helpottaa luvun käyttöä
tilastollisissa testeissä. Laskemme aineistomme keskihajonnan ruutuun C4
kaavalla "=STDEV(A1:A10)". Tulokseksi saamme 2,558211. Keskihajontaa
käytetään mm. yksinkertaisessa t-testissä, jossa verrataan kahden
aineiston keskiarvoja ja keskihajontoja. Karkeasti ottaen t-testin
periaate on tämä: mitä suurempi on keskiarvojen erotus ja mitä pienemmät
keskihajonnat, sitä merkittävämpi on aineistojen ero toisiinsa nähden.
Mikäli tilaston arvot osoittavat taipumusta kehittyä johonkin tiettyyn
suuntaan jollakin tietyllä tavalla, voidaan mahdollisia tulevia arvoja
yrittää ennustaa muodostamalla funktio, joka kuvaa arvojen käyttäytymistä.
Tällöin sovitetaan arvopisteisiin parhaiten sopiva käyrä, jota
kutsutaan regressiokäyräksi tai trendiviivaksi.
Funktiotyyppi, jota arvojen epäillään noudattavan, on arvattava esim.
tilaston kuvaajaa katsomalla. Oikeaa funktiota ei voi mikään ohjelma
varmuudella sanoa, joskin on olemassa joitakin testejä sille, kuinka
luotettavana saatua regressiota voidaan pitää. Piirrämme seuraavassa
Excelin automaattisella trendiviivatoiminnolla kuvaajat lineaarisesti ja
eksponentiaalisesti kehittyvään (tai sellaiseksi oletettuun) aineistoon.
Regressiokuvaajan laskeminen on pitkällinen toimenpide, joka on syytä
jättää tietokoneen suoritettavaksi.
Ensimmäisessä tapauksessa mittaamme auton nopeutta tasaisin väliajoin, kun
autoon vaikuttaa jokin voima, esim. kiihdyttävä moottori. Sijoitamme
A-sarakkeeseen ajanhetket 0-5 ja B-sarakkeeseen auton nopeudet
seuraavasti:
Nyt piirrämme pistediagrammin, jossa aika-akseli on alareunassa ja
nopeusakseli sivureunassa. Tämä voidaan tehdä valitsemalla
taulukko (siis solut A1:stä B6:een) ja painamalla graafintekonappia,
valitsemalla taulukkotyypiksi "XY (Scatter)" ja painamalla suoraan
Finish-nappia. Näin saadaan (muotoiluiltaan tosin karkea) kaavio, joka
esittää mitatut auton nopeudet eri ajanhetkillä. Kuvasta nähdään, että
nopeus kasvaa melkein lineaarisesti eli suoran f(x)=kx+a mukaisesti, missä
k ja a ovat vakioita. Todennäköisesti autoon siis vaikuttaa melko tasainen
voima ja voimme olettaa poikkeamien tasaisesta kiihtymisestä olevan
satunnaisia tai johtuvan mittausvirheistä. Sovitamme nyt regressiosuoran
kuvaamaan kuvitellun auton nopeusfunktion kulkua.
Painetaan kuvaajan jotain arvopistettä, jolloin kaikki arvopisteet saavat
päälleen mustat neliöt. Painetaan sitten arvopisteen kohdalla hiiren
oikeaa nappia ja valitaan avautuvasta pop-up-valikosta "Add Trendline...".
Esiin tulee valintaikkuna, jossa on välilehdet Type ja Options. Koska
haluamme lineaarisen regressiokuvaajan, valitsemme tyypiksi "linear".
Options-välilehdestä valitsemme kohdan "Display equation on chart", jolla
saamme regressiosuoran funktion määrittelyn esiin kuvaajaan. Tämän jälkeen
painetaan "OK". Kuvaajaan piirtyy arvio siitä, miten auton nopeus
suunnilleen kehittyy (Tätä olisi voinut ekstrapoloida Options-välilehden
Forecast-kohdasta). Kuvaajan viereen ilmestyy funktio (y = 2x + 10), jolla
voidaan laskea arvioita auton tuleville nopeuksille, jos kehitys pysyy
samansuuntaisena. Esim. arvioitu nopeus hetkellä 10 olisi 2*10+10=30.
Samaan tapaan voidaan laskea eksponentiaalinen tai mm. polynominen tai
logaritminen regressio, riippuen siitä mitä funktiota meidän on parhaiten
syytä olettaa tilaston arvojen seuraavan. Lineaarinen ja eksponentiaalinen
ovat käytännössä ehkä yleisimmät, sillä meillä saattaa olla esitieto tai-
hypoteesi mitattavaan ilmiöön vaikuttavasta vakiotekijästä (lineaarinen
tapaus) tai ilmiön muutosnopeuden riippumisesta ilmiöstä itsestään
(eksponentiaalinen tapaus). Kuitenkin esim. jos äskeisessä tapauksessa
olisi tarkasteltu auton sijainteja eri aikoina, niitä olisi parhaiten
sopinut kuvaamaan toisen asteen kuvaaja, koska sijainti on nopeuden (joka
oli siis ensimmäistä astetta) integraali.
Muutetaan nyt äskeisen taulukon arvot kuvaamaan erään bakteeripopulaation
havainnoista arvioitua kasvua ajanhetkinä 0-5, seuraavasti:
Piirretään tästä uusi XY-kuvaaja ja tarkastellaan sen pisteitä. Pisteiden
asettuminen näyttää eksponentiaaliselta, samaten tilanne on mahdollinen
eksponentiaalisen kasvun tilanne: jokainen uusi bakteeri pyrkii
lisääntymään. Tällä kertaa piirrämme eksponentiaalisen regressiokäyrän
menetellen muuten samoin kuin viimeksi, mutta valiten "Add Trendline"
-ikkunan Type-välilehdestä tyypin "Exponential".
Kuvan pitäisi nyt näyttää tältä. Käyrä sopi pisteisiin varsin hyvin eli
ilmeisesti kysymys on eksponentiaalisesta kasvusta. Bakteeripopulaation
kokoa hetkellä x voi arvioida sijoittamalla kuvan kaavaan x:n paikalle
ajanhetki ja ratkaisemalla y.
Harjoitus 9. Laadi hyvin tuntemistasi kanssaopiskelijoista
ikätilasto. Mikä on tilaston keskiarvo? Entä moodi, mediaani ja
keskihajonta? Onko moodin ja keskiarvon tai mediaanin ja keskiarvon
poikkeama suuri? Mitä nämä poikkeamat mielestäsi kuvastavat? Entäpä
keskihajonta?
Harjoitus 10. Taimen pituudet peräkkäisinä päivinä (mitattuna
klo 12 päivällä) olivat 1,2cm, 1,8cm, 2,3cm, 3,0cm, 3,7 cm ja 4,3cm.
Muodosta aineistosta taulukko ja kuva. Minkälaisen regressiokuvaajan
sijoittaisit kuvaajaan? Jos ensimmäinen päivä oli numero 0, kuinka pitkä
arvioit taimen olevan päivänä 20 regressiota piirtäessäsi saamasi funktion
mukaan?
Tutustutaan matriisien perusoperaatioihin Excelillä.
Eräs Excelin vahvuus on siinä, että kaavoja voidaan kopioida ruudusta
toiseen helposti niin, että viittaukset muihin soluihin siirtyvät mukana.
Tämän avulla matriisien yhteenlaskun ja skalaarikertolaskun suorittaminen
on äärimmäisen helppoa.
Luodaan kaksi matriisia yksinkertaisesti kirjoittamalla lukuja taulukkoon.
(Mitäpä muutakaan matriisi on kuin lukuja taulukossa?)
Lasketaan ensin nämä matriisit yhteen. Yhteenlasku tapahtuu alkioittain,
joten kirjoitetaan tulosmatriisin ensimmäiseen soluun ensimmäisten
alkioiden summa: =A2+E2. Tämän jälkeen kopioidaan kaavaa oikealle ja alas
koko matriisin kokoiseksi. Excel muuttaa viittaukset juuri halutulla
tavalla.
Kerrotaan sitten matriisi A luvulla 7. Kirjoitetaan jälleen haluttu kaava
=7*A2 tulosmatriisin ensimmäiseen soluun ja kopioidaan matriisin
kokoiseksi.
Matriisien kertolasku on hieman vaikeampi operaatio. Siihen Excel tarjoaa
valmiin funktion MMULT. Kaava =MMULT(...) on niin sanottu
taulukkokaava (array formula), jonka tuloksen näyttämiseen
tarvitaan useampi taulukon solu. (Tavallisen kaavan tuloshan näkyy yhdessä
solussa.) Taulukkokaavojen syöttäminen ei ole aivan ongelmatonta.
Matriisit A ja B ovat sellaisia, että ne voidaan kertoa keskenään.
Kirjoitetaan tulosmatriisin ensimmäiseen soluun kaava =MMULT(A2:C4;E2:G4)
ja painetaan Enter. Tuloksesta näkyy nyt vain yksi solu. Tämän jälkeen
suoritetaan peräkkäin seuraavat toimenpiteet:
Taulukkokaavan tunnistaa siitä, että muokkausrivillä olevan kaavan
ympärillä näkyy aaltosulut { }. Taulukkokaavoja ei voi muokata niiden
luomisen jälkeen. Jos näin yrittää tehdä, ohjelma antaa virheilmoituksen:
"You cannot change part of an array." Tästä tilanteesta pääsee pois
painamalla Esc. Jos taulukkokaavan on syöttänyt väärin, solu täytyy
tyhjentää ja kaava kirjoittaa uudestaan.
Käänteismatriisin laskemiseksi Excelissä on kaava MINVERSE. Tämän on myös
taulukkokaava, jota käytetään samalla tavoin kuin kertolaskukaavaa.
Lasketaan esimerkiksi A:n käänteismatriisi. Kirjoitetaan sitä varten kaava
=MINVERSE(A2:C4), maalataan sopivan kokoinen (3x3) alue, painetaan F2 ja
lopulta Ctrl+Shift+Enter. Käänteismatriisi ilmestyy soluihin.
Taulukkokaavoja voi kopioida samalla tavoin vetämällä kuin tavallisiakin
kaavoja. Lasketaan esimerkiksi matriisin A potensseja. Nämä määritellään
samalla tavoin kuin luvuillakin, eli A^2=AA, A^3=AAA, jne. Huomaa
kuitenkin, että vain neliömatriiseja voidaan korottaa potenssiin.
Voimme laskea A:n peräkkäisiä potensseja kertomalla edellinen potenssi
aina uudestaan A:lla. Kirjoitetaan sitä varten aivan A:n alapuolelle
(jättämättä riviäkään väliin) kaava, jossa yläpuolella oleva matriisi
kerrotaan A:lla. Kaavaksi tulee siis (kuvan mukaan)
=MMULT($A$2:$C$4;A2:C4). Huomaa, että ensimmäiseen viittaukseen tulee
dollarimerkit. Tämä sen takia, että kaavaa kopioitaessa syntyvissä
kaavoissa kerrottaisiin aina alkuperäisellä matriisilla A.
Tämän jälkeen maalataan sopiva alue (3x3-matriisi), ja painetaan F2 ja
Ctrl+Shift+Enter. Matriisin pitäisi ilmestyä näkyviin. Sitten vain
kopioidaan kaavaa alaspäin vetämällä, jolloin syntyy matriisin potensseja.
Harjoitus 11. Tarkastellaan matriiseja
Harjoitus 12. Ratkaise yhtälöryhmä
Harjoitus 13. Neliömatriisin determinantti on matriisia
kuvaava luku, joka voidaan laskea Excelin kaavalla MDETERM (tämä ei siis
ole taulukkokaava). Tutki helppojen 2x2-matriisien avulla, miten kahden
matriisin tulon determinantti riippuu tekijämatriisien determinanteista.
Entä miten käänteismatriisin determinantti riippuu alkuperäisen matriisin
determinantista?
Maple on sekä symboliseen että numeeriseen laskentaan sopiva
matematiikkaohjelma. Sen pääpaino on kuitenkin symbolisessa laskennassa.
Maple osaa suorittaa toisinaan hyvinkin vaikeita symbolisia matemaattisia
toimituksia.
Maple löytyy ainakin keskustan, Kumpulan laitosten ja biotieteen (?)
koneista kohdasta "Math and Statistics". Jolli Maplea ole käyttämääsi
koneeseen asennettu, sitä voi etsiskellä "Installations"-kansiosta ja
asentaa. Maplea voi käyttää eri käyttöliittymillä, joista nyt käytämme
monipuolisinta, Maplen varsinaista käyttöliittymää. Tämä käynnistetään
kuvakkeesta "Maple 9.5".
Maple näyttää käynnstyessään "Päivän vinkki" -ikkunan. Suljettuasi sen
saat käyttöösi tyhjän Maple-työtilan, jonka alussa on uusi tyhjä kenttä
merkittynä hakasella ja nuolella [>. Kenttään voit kirjoittaa
periaatteessa millaisia tahansa matemaattisia lausekkeita tai Maplen
komentoja. Kun painat kentässä ENTERiä, Maple suorittaa kenttään
kirjoittamasi komennot ja laskut ja siirtyy uuteen kenttään. Kirjoituksesi
tulee Mapleen punaisena ja Maple vastaa sinisellä värillä. Huomaa, että
Maplen vastaukset muistuttavat enemmän perinteistä matemaattista
kirjoitusasua kuin käyttäjän kirjoittamat, Maplelle ymmärrettävät
lausekkeet.
Voit lisätä vanhojen kenttien väliin uuden painamalla ylhäällä
työkalurivissä olevaa "[>"-näppäintä. Viereisellä "T"-näppäimellä voi
luoda "tekstikentän", johon voi kirjoittaa vain kommentteja tai
muistiinpanoja. Tällaiseen kenttään kirjoittamasi teksti näkyy mustana
eikä punaisena, eikä Maple yritä suorittaa sitä.
Maplelle syötettävien lausekkeiden ja komentojen yhteydessä on syytä
huomata seuraavat seikat:
Maple laskee tavalliseen tapaan peruslaskutoimitukset summan, erotuksen,
tulon ja osamäärän (merkit +, -, *, /). Kokeillaan laskemalla 15*263.
[> 15*263; [ENTER]
Maple ilmoittaa tuloksen 3945. 1.2*5.6 puolestaan on Maplen mukaan 6.72.
1/2:n tuloksen Maple taas ilmoittaa murtolukumuodossa. On huomattava, että
Maple laskee oletusarvoisesti kaikki jako- ja juurilaskut (ja kaikki
muutkin laskut) symbolisesti, siis ei desimaaliluvuilla kuten
laskimet, vaan tarkoilla arvoilla (paitsi jos käyttäjän syöttämät luvut
ovat desimaalilukuja). Siksi murtoluvut pysyvät Maplen
laskuissa murtolukuina, juuret juurina ja irrationaaliluvut
irrationaalilukuina, eikä niitä ilmoiteta laskujen tuloksissa
likiarvoina.
Potenssiin korotus tehdää Maplessa operaattorilla ^, jonka saa
näppäinyhdistelmällä SHIFT-¨ ja painamalla tämän jälkeen välilyöntiä.
Neliöjuuren voi ottaa komennolla sqrt(juurrettava) ja mielivaltaisen
juuren korottamalla murtopotenssiin tai komennolla root(juurrettava,
juuren luku) [tätä pitää tarkistaa!]. Huomaa, että Maple voi esim.
juurilaskuissa ja vallankin mutkikkaammissa toimituksissa antaa
kompleksiratkaisuja, jotka tunnistaa mukana olevasta isosta
I-kirjaimesta. Tämä on Maplessa ns. imaginääriyksikön symboli, eikä
sitä käytetä muuttujan nimenä. Koska kurssimme koskee reaalisia
funktioita, voimme jättää kompleksivastaukset kylmästi huomiotta.
Desimaalilikiarvon Maplen antamalle murto- tai irrationaalivastaukselle
saa evalf-funktiolla. Kirjoitetaan
[> evalf(sqrt(2)); [ENTER]
Näytölle tulee kakkosen neliöjuuren likiarvo kymmenen desimaalin
tarkkuudella. (Tämä on Maplen oletustarkkuus, jota voi halutessaan säätää
digits-komennolla.)
Logaritmien laskeminen Maplella onnistuu komennolla log. Pelkkä
log(luku) tarkoittaa Maplessa luonnollista logaritmia, jonka kantaluku on
e. Mielivaltainen logaritmi ilmaistaan muodossa log[a](luku), missä
a on logaritmin kantaluku. Hakasulkeet löytyvät painamalla pohjaan "Alt
Gr" -näppäin ja sitten 8:aa ja 9:ää. Kymmenkantaiselle logaritmille
Maplessa on oma komento log10. Logaritmit ovat yleensä
irrationaalisia, joten Maplen vastaus vaikkapa käyttäjän lausekkeeseen
"log(5)" on yksinkertaisesti "log(5)". Logaritmin desimaalilikiarvo
saadaan taas kirjoittamalla lauseke evalf-funktion jälkeen
sulkeisiin.
Sini, kosini ja tangentti lasketaan Maplessa funktioilla sin,
cos ja tan. Arvot ovat jälleen tavallisesti irrationaalisia,
joten vastauksena vaikkapa lausekkeeseen "sin(3)" Maple antaa "sin(3)".
Maplessa on määriteltynä vakio &pi, joka ilmaistaan "Pi". Esimerkkinä
Maplen symbolisen laskennan älykkyydestä voimme ottaa sinin ja kosinin
piistä:
[> sin(Pi);
[> cos(Pi);
Maple "ymmärtää" piin merkityksen trigonometrisissä (ja monissa muissakin)
yheyksissä ja osaa laskea sen avulla tarkkoja arvoja. Maple osaa myös
ilmaista monen laskutomiituksen tuloksen piin, ei piin likiarvon
avulla. Huom! Maple laskee trigonometriset funktiot radiaaneilla.
Asteet voi muuttaa radiaaneiksi kertomalla piillä ja jakamalla 180:llä.
(Käytä tällöin Maplessa "Pi":tä jos haluat tarkan arvon!)
Matemaattiselle vakiolle e Maplella ei ole varsinaista omaa
merkintää, vaan sitä käsitellään eksponenttifunktion arvona kohdassa 1.
Tähän palaamme seuraavassa luvussa.
Maple noudattaa normaaleja laskujärjestyssääntöjä: ensin logaritmit ja
trigonometriset funktiot, sitten potenssit [tarkista tämä], sitten kerto-
ja jakolaskut ja lopuksi yhteen- ja vähennyslaskut. Laskujärjestystä voi
muuttaa sulkeilla (), joita käytetään tavalliseen tapaan. Käytämme vain
tavallisia sulkuja määrittämään laskujärjestystä, jotta vältämme
sekaannukset joidenkin Maplen komentojen käyttämien erikoissulkujen
kanssa.
Maple-työtilan - eli kaiken mitä olet tehnyt - voi tallentaa kuten minkä
tahansa dokumentin valitsemalla File-valikosta komennon "Save as...".
Ennestään tallennetun työtilan voi tallentaa vanhan päälle samasta
valikosta Save-komennolla. Työkalurivistä löytyvä "!!!"-nappi voi myös
joskus olla hyödyksi: se lukee ja suorittaa uudelleen koko työtilan laskut
ja komennot. Lisäksi Maplessa on erittäin laaja, syvällinen ja toimiva
opastus (Help-valikosta), jonka käyttäminen tosin vaatii aluksi pientä
totuttelua.
Harjoitus 1. Laske Maplella tarkat arvot ja likiarvot (evalf:llä):
285-766, Pi*(-11.3), 14^(4-1), 122/739, sqrt(10), 8^(2/3), 8^2/3,
log[2](16), log(-cos(Pi)), sin(Pi/4), tan(1). Kokeile numeroiden
muuttamista kenttiin ja laske uudelleen. Tallenna.
Harjoitus 2. Syötä Mapleen lausekkeet a+b, a*b/a, a^(b/c),
sin(a-a). Muista puolipisteet ja paina joka lausekkeen jälkeen ENTER.
Miten Maple toimii?
Maple käsittelee mitä tahansa mielivaltaista kirjainta tai
kirjainyhdistelmää, jollei se ole Maplessa erikseen määritelty funktio,
komento tai vakio, muuttujana ja ratkaisee matemaattiset ongelmat
symbolisesti pitäen muuttujat muuttujina, ellei niille anneta joitakin
arvoja. Maplessa voi myös tallentaa lausekkeita kirjaimiin tai
kirjainyhdistelmiin, siis antaa lausekkeille nimiä, ja antaa Maplen sitten
käsitellä näitä lausekkeita. Lauseke ei ole sama asia kuin funktio,
joita opimme luomaan seuraavassa luvussa.
Annamme lausekkeelle x^2+2x nimen k. Tämä tehdään ns.
sijoitusoperaattorilla ":=". Kirjoitamme siis Mapleen
[> k := x^2+2*x; [ENTER]
Kone antaa sijoitukselle vahvistuksen. Voimme kokeilla, mitä tuli
sijoitettua kirjoittamalla yksinkertaisesti "k;" ja painamalla ENTER.
Huomaa, että "k(3);" ei anna lausekkeen arvoa siten, että x:n paikalle
olisi sijoitettu 3, sillä k ei ole funktio. Nimetylle lausekkeelle voidaan
kuitenkin tehdä Maplessa monenlaisia operaatioita ja se voidaan korvata
uudella lausekkeella milloin vain sijoittamalla uudestaan. Tällöin vanha
lauseke katoaa. Huomaa, että Maple käsittelee kulloinkin niitä
tallennettuja lausekkeita, jotka on ajallisesti viimeksi
määritelty. Jos liikut ympäri työtilaa ja määrittelet asioita uudelleen,
voi aiemmin kirjoitettujen kenttien uudelleen ajaminen tuottaa yllättäviä
tuloksia, kun niissä olevat lausekkeet ovatkin muuttuneet. Se, että
näytöllä lukee jotain määrittelytä, ei takaa, että ne olisivat enää
voimassa; voimassa on aina viimeisenä ENTERillä vahvistettu määrittely,
jos sama kirjain on näytöllä määritelty moneksi eri asiaksi. Mikäli
määrittelyissä tulee sekaannuksia, tilanteen voi esim. nollata
restart-komennolla, joka käynnistää Maplen matematiikkamoottorin
uudelleen ja hävittää kaikki määrittelyt. Sen jälkeen haluamiaan kenttiä
voi ajaa ENTERillä uudelleen saadakseen voimaan niihin kirjoitetut
määrittelyt.
Lausekkeita voi esim. yhdistää. Kirjoitamme
[> r := k+3/x-y; [ENTER]
Nyt Maple sijoittaa vanhan k-lausekkeen uuteen r-lausekkeeseen k:n
paikalle.
Lausekkeesta voidaan muodostaa yhtälö ja se voidaan ratkaista
solve-komennolla. Esim. "solve(k=3, x);" ratkaisee x:n yhtälöstä
x^2+2x=3. Tässä tapauksessa Maple antaa automaattisesti kaikki ratkaisut,
joskus se vaatii erillisen komennon (sikäli kuin Maple aina edes pystyy
kaikkia ratkaisuja löytämään). Ratkaisun desimaalilikiarvot saa taas
evalf:llä.
Lausekkeen avulla voidaan myös piirtää lausekkeen kuvaaman funktion
kuvaaja. Tämä voidaan tehdä myös suoraan funktiolle aivan samalla
tavalla. Piirrämme nyt Maplella pari kuvaajaa.
Kuvaajat piirretään komennolla "plot". Plotin jälkeen tulee suluissa
joukko argumentteja, joista tässä käytämme neljää. Aluksi kirjoitetaan
piirrettävän funktion lauseke, sitten x-akselin arvot, joiden alueella
kuvaaja piirretään. Loput kaksi argumenttia käymme läpi piakkoin.
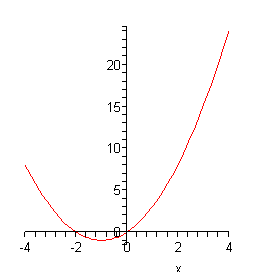
Piirretään nyt funktion f(x)=x^2+2x kuvaaja välillä x=[-4,4]. Meillä on
funktion riippuvuussääntö lausekkeessa k, joten voimme kirjoittaa
[> plot (k, x=-4..4); [ENTER]
Maple skaalaa pysty- eli y-akselin automaattisesti kuvaamaan parhaiten
funktion kulkua. tulokseksi saamme ylöspäin aukeavan paraabelin. Kuvaajan
kokoa voi säätää vetämällä hiirellä valkeista pikku neliöistä, jotka
nkyvät kuvan ympärillä, kun hiiri viedään sen päälle. Huomaa, että Maple
joutuu piirtämään kuvaajan numeerisesti, joten siinä "näkyviin"
arvoihin ei voi eksaktissa tarkastelussa tietenkään luottaa. Kuten mikä
tahansa komento, myös kuvaajan piirtäminen voidaan suorittaa uudestaan
uusilla argumenteilla samassa kentässä siten, että argumentteja käydään
muuttamassa ja painetaan taas ENTER.
Sijoitetaan uusi lauseke.
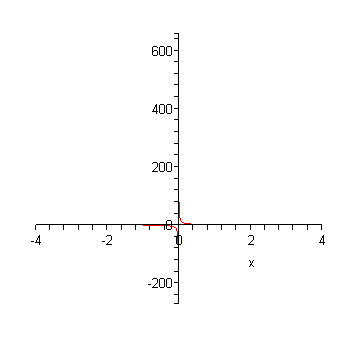
[> g(x)=1/x; [ENTER]
ja kirjoitetaan seuraava piirtokomento:
[> plot (g(x), x=-4..4); [ENTER]
Nyt huomataan kaksi ongelmaa: Ensinnäkin y-akseli skaalautuu niin
suurimittakaavaiseksi, ettei kuvaajan lukeminen ole enää helppoa. Toiseksi
Maple piirtää suoran pystyviivan kohtaan x=0, missä funktio 1/x ei
oikeasti ole edes määritelty. (Tämä ei itse asiassa suoraan kuvasta näy,
koska mittakaava on niin suuri. Ongelman voi kuitenkin havaita menemällä
käyrän päälle hiirellä, jolloin kuvaaja vahvistuu.) Nämä molemmat ongelmat
voidaan poistaa antamalla plot-komennolle kaksi lisäargumenttia. Y-akseli
pitää skaalata käsin, koska Maplen automaattiskaalaus menee
liiallisuuksiin hyvin suurten ja hyvin pienten arvojen näyttämisessä ja
kohdat, joissa funktio ei ole määritelty sekä mahdolliset
epäjatkuvuuskohdat (joihin myös tulisi suora pystyviiva) on löydettävä.
Tämä tuottaa Maplelle hieman lisätöitä, mutta ohjelma suoriutuu niistäkin
nopeasti moderneissa koneissa.
[> plot (g(x), x=-4..4, y=-10..10, discont=true); [ENTER]
Nämä lisäehdot määrittelevät y-akselista nätettäväksi välin [-10, 10] ja
pakottavat Maplen etsimään em. kohdat funktiosta ennen piirtämistä
(discontinuity=epäjatkuvuus). Nyt kuvaajan piirtäminen onnistuu
tyylikkäästi. Huomaa, että g(x) ei ole vieläkään Maplen kannalta funktio
vaan lauseke, joten jos nyt kirjoitat "g(2);" ja painat ENTER, kone vastaa
"g(2)", koska se ei voi tietää, että tarkoitat kakkosella erästä x:ää.
Piirrämme vielä lopuksi useampia funktioita samaan kuvaan ja sijoitamme
funktion lausekkeen suoraan plot-komentoon.
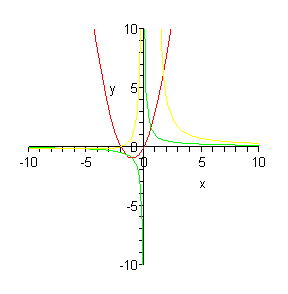
[> plot ({k, g(x), (2*x+4)/(x^2-x)}, x=-10..10, y=-10..10, discont=true);
[ENTER]
Piirsimme kahden edellisen lausekkeen määrittämät funktiot sekä
ylimääräisen rationaalifunktion, jonka lauseke on kirjoitettu suoraan
plot-komentoon. Piirrettävien funktioiden lausekkeet kirjoitetaan tällöin
aaltosulkeiden (Alt Gr + 7 ja Alt Gr + 0) sisään ja erotetaan pilkuilla.
Muutoin toimittiin jo opittuun tapaan. Maple piirtää eri funktiot kuvaan
eri väreillä ja paksuntaa funktion kuvaajaa, jos liikutat hiiren
osoittimen sen päälle. Näin on helppo ottaa esiin haluttu kuvaaja hyvinkin
monen samaan kuvioon piirretn kuvaajan joukosta.
Harjoitus 3. Syötä Mapleen lausekkeet p=x^2-x ja t=p/3x-4. Piirrä
ne eri kuviin ja samaan kuvaan. Skaalaa järkevästi ja estä Maplea
tekemästä "epäjatkuvuusvirhettä". Kokeile, miltä kuvat näyttävät
erilaisilla skaalauksilla.
Harjoitus 4. Piirrä funktion f(x)=2x^2-4 kuvaaja. Arvioi kuvaajan
perusteella funktion nollakohtia ja ratkaise ne solve-komennolla tarkkoina
arvoina ja likiarvoina.
Funktiot voi määritellä Maplessa symbolisesti sijoitusoperaattorin ja
"nuolen" (->) avulla. Tätä nuolta ei pidä sekoittaa luennoilla ja
materiaalissa funktion määrittely- ja maalijoukosta kertovan merkinnän
nuoleen. Maplessa funktion määrittelyyn käytetty nuoli merkitsee samaa
kuin toisinaan matemaattisessa tekstissä esiintyvä nuoli, jonka alussa on
pystyviiva (
[> f := x -> x^3-2*x; (Enää en merkitse ENTERin painalluksia näkyviin.)
Huomaa, että funktion nimen jälkeen ei merkitä sulkuihin muuttujaa.
Funktio toimii nyt millä muuttujilla tai luvuilla tahansa. Kokeillaan:
[>f(t-2);
(t-2)3-2t+4
Huomaa, että Maple ei kerro auki eikä sievennä lausekkeita
automaattisesti. Sievennys sujuu
simplify(sievennettävä)-komennolla ja auki kertominen
expand(auki kerrottava) -komennolla. Voit kokeilla tätä. (Tässä
tapauksessa molemmat komennot antavat saman tuloksen.)
Voit myös määritellä vakiofunktion:
[> f := x -> 3;
Tällöin funktio saa saman arvon riippumatta muuttujasta.
Tutkitaan nyt muutamia funktioita Maplella. Muodostetaan funktio
g(x)=(5*x^2+2*x)/(3*x^2-x) ja piirretään sen kuvaaja.
[> g:=x->(5*x^2+2*x)/(3*x^2-x);
(Välilyöntien käyttö Maplessa on yhdentekevää; niitä on syytä käyttää
silloin kun ne selventävät asiaa kirjoittajalle itselleen.)
[> plot(g(x), x=-10..10, y=-5..5, discont=true);
Huomaa, että funktion g avulla voidaan muodostaa lauseke g(x), jonka
plot-komento voi sitten piirtää halutuilla x. Discont-termi on tällä
kertaa välttämätön, sillä kyseessä on rationaalifunktio, jonka
määrittelyjoukko katkeaa tarkastelualueella. Kuvaajassa näkyy nyt yksi
selkeästi määrittelyjoukkoon kuulumaton kohta. Ilmeisesti funktio ei ole
määritelty nollassa (kokeile nimittäjän arvoa kun x=0), mutta kuvaajasta
näkemämme kohta on jokin muu. Funktiolla on kaksi reaalista kohtaa,
joissa se ei ole määritelty, x=0 ja x=1/3, mutta tätä ei voi päätellä
suoraan kuvaajasta, sillä pisteeseen x=0 ei liity muuten erikoista
käyttäytymistä. (Ts. funktio ei kasva ja/tai vähene rajatta sen ympärillä.
Funktiolla on jopa raja-arvo ko. pisteessä!) Nimittäjän nollakohdat pitää
siis aina ratkaista, esim. Maplella. Näin:
[> solve(3*x^2-x=0, x);
Ratkaiseminen käsinkin on tässä tapauksessa helppoa.
Määritellään eksponenttifunktio ex. Kuten sanottu, Neperin
luvulle e ei ole Maplessa omaa merkintää, vaan se on eksponenttifunktion
arvo kohdassa 1. Funktio on exp(eksponentti) ja e ilmaistaan
Maplessa täten kirjoittamalla "exp(1)". Määritellään:
[> h := x -> exp(x);
Määritellään sitten toisenlainen eksponenttifunktio, jonka kantaluku on
pienempi kuin 1.
[> i := x -> exp(-x);
Tämä funktio on sama kuin (1/e)^x, koska
e-x=e-1*x=(e^-1)^x=(1/e)^x. Piirretään molemmat
funktiot samaan kuvaan.
[> plot ({h(x), i(x)}, x=-4..4);
Funktioiden nähdään kasvavan ja vähenevän nopeasti. Näillä funktioilla ei
ole nollakohtia, vaan ne ovat aina aidosti positiivisia, minkä voi testata
solve-komennolla (mitään ratkaisua ei pitäisi tulla). Eksponenttifunktiot
mielivaltaisella kantaluvulla voi ilmaista yksinkertaisesti x -> a^x,
missä a on kantaluku.
Määrätään ja piirretään vielä logaritmifunktio samaan kuvaan exp(x):n
kanssa:
[> j := x - > log(x);
(Tämä oli siis luonnollinen logaritmi.)
[> plot({h(x), j(x)}, x=-4..4, y=-4..4);
Huomataan, että luonnollisen logaritmin kuvaaja on sama kuin e-kantaisen
eksponenttifunktion peilattuna viiston suoran y=x suhteen. Näin onkin aina
käänteisfunktioiden laita.
Lopuksi määrittelemme ja piirrämme vielä sinifunktion k(x)=3sin(3x).
[> k := x -> 3*sin(3*x);
[> plot (k(x), x=-10..10);
Muotoilemalla kuvaajaa hieman siitä saadaan tällainen:
Kuvaajasta nähdään likimäärin, että funktion arvojoukko on [-3,3]. Tämä
voidaan helposti todeta funktiota tutkimalla. Funktion jakso on kolme
kertaa normaalin sinifunktion jaksoa tiheämpi: nollasta 2&pi :hin
(x-akselilla hieman kuuden jälkeen) näyttäisi mahtuvan kolme jaksoa.
Sinifunktion nollakohdat voi päätellä yhdestä Maplen antamasta
ratkaisusta:
[> solve(k(x)=0, x);
Maplen saa myös näyttämään kaikki ratkaisut. Tätä varten pitää asettaa
Maplen ympäristömuuttuja _EnvAllSolutions arvoon "true".
[> _EnvAllSolutions:=true;
Tämän jälkeen mennään uudelleen edelliselle solve-riville ja painetaan
ENTER.
Koneen antama vastaus 1/6&pi+1/3&pi _Z1~ tarkoittaa, että ratkaisut ovat
1/6&pi + vakio * 1/3&pi, missä vakio on kokonaisluku (siitä kirjain Z).
Alaviiva osoittaa, että kyseessä on Maplen muodostama
vapaavalintainen vakio, ykkönen Z:n perässä taas kertoo, että kyseessä
oli ensimmäinen tällä laskentaistunnolla käyttöön otettu tämäntyyppinen
vakio ja aaltoviiva kertoo, että vakio ei voi olla mitä tahansa (tässä
tapauksessa sen on oltava kokonaisluku).
Harjoitus 5. Määrittele ja piirrä funktiot f(x)=x^15,
g(x)=x^3-2*x^2+x, h(x)=x^3-2*x^2+x+0.01,
i(x)=-(3x^2+2x)/(2x^2+3x), j(x)=e^(x^2) ja k(x)=tan(x). Ota piirtäessäsi
huomioon mahdolliset määrittelyjoukon katkeamiset ja etsi järkevä
skaalaus. Mitä voit kuvaajien perusteella sanoa funktioiden nollakohdista
ja määrittelystä? Etsi g:n, h:n ja k:n kaikki nollakohdat (lukuunottamatta
kompleksisia) ja määritä i:n määrittelyjoukko.
Maple laskee funktion tai lausekkeen raja-arvon limit-komennolla.
Komennon jälkeen kirjoitetaan sulkeisiin ensin lauseke (joka voi siis olla
myös funktion arvo jollain muuttujalla, esim. "f(x)") ja sitten muuttuja,
jonka arvolla raja-arvoa etsitään, yhtäläisyysmerkki ja raja-arvon
etsimispiste. Etsitään funktion f(x)=x^2 raja-arvo kohdassa 3.
[> limit (x^2, x=3);
Nähdään, että tässä tapauksessa raja-arvo on sama kuin funktion arvo.
Rationaalifunktion raja-arvo määrittelyjoukon ulkopuolisessa pisteessä
saattaa olla olemassa. Näin on yleensä asian laita, jos kuvaajasta katsoen
funktio näyttäisi jatkuvan pisteen yli. Määritellään
[> f:=x->(5*x^2+2*x)/(3*x^2-x);
ja lasketaan
[> limit (f(x), x=0);
Tulokseksi saadaan -2, kuten kuvaajakin antaa ymmärtää. Joskus raja-arvo
voi olla ääretön.
[> limit (abs(1/x), x=0);
Halutessasi voit piirtää tästä kuvaajan! Funktion arvot kasvavat
rajatta kummaltakin puolelta, kun x lähestyy nollaa.
Raja-arvoa voi myös tutkia äärettömyydessä asettamalla x=infinity
tai x= -infinity (negatiivinen äärettömyys). Monet funktiot
kasvavat
tai vähenevät rajatta tällaisessa tarkastelussa, mutta esim.
[> limit (f(x), x=infinity);
ja
[> limit (f(x), x=-infinity);
antavat molemmat tuloksen 5/3.
Aina raja-arvo ei ole määritelty. Lasketaan esim.
[> limit (1/x, x=0);
Kone vastaa "undefined", määrittelemätön, sillä funktion arvot vähenevät
rajatta lähestyttäessä toiselta puolen pistettä x=0 ja kasvavat rajatta
lähestyttäessä toiselta puolen.
Tutkimme vielä tapausta, jossa raja-arvo kertoo meille kahden funktion
suhteesta. Laskemme raja-arvon limx &rarr &infin (P(x)/e^x),
missä P(x) on polynomifunktio, jollakin P(x):llä. Valitaan P(x)=x^3.
[> limit(x^3/exp(x), x=infinity);
Kone saa vastaukseksi 0. Vaihdellaan x^3:n paikalle eri polynomifunktioita
ja huomataan, että tulos on aina sama. Tämä johtuu siitä, että
eksponenttifunktio kasvaa lopulta aina mitä tahansa polynomifunktiota
nopeammin, kun siirrytään eteenpäin x-akselilla, ja eksponentiaalifunktion
arvot tulevat mielivaltaisen moninkertaisiksi vastaaviin polynomifunktion
arvoihin nähden, kun x:ää kasvatetaan. Siksi tällaisen osamäärän raja-arvo
äärettömyydessä on 0.
Harjoitus 6. Etsi rationaalifunktion f(x)=(x^3-2x^2)/(4x^3+x^2)
määrittelyjoukosta puuttuvat pisteet ja laske funktion raja-arvo niissä,
jos se löytyy.
Harjoitus 7. Ota selvää, miten edellisen tehtävän funktio
sekä funktio g(x)=e^x käyttäytyvät äärettömyydessä ja miinus
äärettömyydessä. Entä mikä on logaritmifunktion raja-arvo nollassa?
Mieti ensin ja laske sitten Maplella.
Harjoitus 8. Mitkä ovat tangenttifunktion raja-arvot pisteessä
π/2 ja äärettömyydessä? Onko niitä? Miksei?
Maple derivoi ja integroi symbolisesti määritelmien avulla. Varsinkin
integraalifunktioiden ratkaisemiseen Maple on erittäin tehokas työkalu
ihmisaivoihin verrattuna. Maplen derivaattaoperaatio diff
suoritetaan aina lausekkeelle (joka voi siis myös olla funktio ja sen
muuttuja suluissa) ja se palauttaa arvona lausekkeen. Maplessa on myös
toinen derivaattaoperaattori D, jota emme tällä kurssilla tarvitse.
Tämä operaattori käsittelee suoraan funktioita.
Derivointi kirjoitetaan muodossa diff(lauseke, muuttuja). Muuttuja on se
muuttuja, jonka suhteen derivoidaan, kurssillamme siis funktion ainoa
muuttuja. Derivoimme seuraavaksi polynomifunktion.
[> f := x -> x^3+3*x^2+4*x+1;
[> diff (f(x), x);
Kone antaa vastaukseksi funktion derivaatan 3x^2+6x+4. Voimme tarkistaa
tuloksen laskemalla erotusosamäärän raja-arvon.
[> limit ((f(x+h)-f(x))/h, h=0);
Tutkitaan nyt kuvasta derivaatan suhdetta alkuperäiseen funktioon.
Valitaan funktioksi f(x)=x^2 ja piirretään kuvaan sen ensimmäinen ja
toinen derivaatta. Toinen derivaatta voidaan ilmaista Maplelle kahdella
tavalla: diff(f(x), x, x) (derivoidaan kaksi kertaa x:n suhteen) tai
diff(f(x), x$2) (lyhennysmerkintä).
[> f := x -> x^2;
[> plot({f(x), diff(f(x), x), diff(f(x), x$2)}, x=-4..4);
Ensimmäinen derivaatta näkyy tässä keltaisena viivana ja toinen punaisena.
Kuvio havainnollistaa sitä, että derivaatta kuvaa funktiolle piirretyn
tangentin kulmakerrointa. Kun liikutaan f(x):ää pitkin vasemmalta
oikealle, sen jyrkkyys (eli kulmakerroin) kasvaa tasaisesti (kun oletamme,
että laskevan funktion jyrkkyys on negatiivinen). Niinpä derivaatan
kuvaaja on tässä tapauksessa nouseva suora.
Funktion toinen derivaatta on taas tämän nousevan suoran derivaatta. Sen
jyrkkyys on kaikkialla sama (kulmakerroin 2), joten f(x):n toinen
derivaatta on vakiofunktio 2. Kolmas derivaatta olisi kaikkialla 0, ja
itse asiassa minkä tahansa polynomifunktion n+1:s derivaatta (missä n on
polynomin aste) on kaikkialla 0.
Funktion derivaatta ei ole välttämättä kaikkialla määritelty. Esim.
funktiolla g(x)=1/x ei ole derivaattaa kohdassa 0, koska koko funktiota ei
ole siinä määritelty. Tämä voidaan todeta derivoimalla ja sijoittamalla
derivaattaan x=0.
[> g := x -> 1/x;
[> diff(g(x), x);
Derivaatta ei saa arvoa, jos vastaukseen (-1/x^2) sijoitetaan x=0.
Derivaatan nollakohtien ratkaiseminen on hyödyllistä monissa
matemaattisissa ongelmissa, kun etsitään funktion ääriarvoja jollakin
välillä. Käytännössä tämä onnistuu solve-komennolla. Jos funktio on
vaikkapa f(x)=x^3-2x, saadaan sen derivaatan nollakohdat näin:
[> f := x -> x^3-2*x;
solve(diff(f(x), x)=0, x);
Näin saaduista nollakohdista on sitten valittava se, joka
tehtävän tarkasteluvälille osuu. Trigonometristen funktioiden tapauksessa
Maple antaa taas vain yhden ratkaisun, ellei _EnvAllSolutions-muuttujaa
ole ensin määritelty arvolle "true". Muut ratkaisut voi laskea käsin tai
Maplella muuttujan arvon asettamisen jälkeen.
[> f := x -> sin(2*x);
[> _EnvAllSolutions := true;
[> solve(diff(f(x), x)=0, x);
Tässä ratkaistiin funktion f(x)=sin(2x) derivaatan kaikki nollakohdat.
Ennen siirtymistä integraaleihin piirrämme vielä derivaatan avulla
funktion f(x)=x^2 kuvaajalle sivuajan (tangentin) pisteeseen x=2.
Sivuajan johtaminen käsitellään Excel-osiossa kohdassa Newtonin menetelmä.
[> f := x -> x^2;
[> diff(f(x), x);
Tulokseksi saadaan 2x.
[> df := x -> 2*x; (määrätään, että funktion derivaatta on "df". Tässä
olisi voitu käyttää myös D-operaattoria: "df := D(f)".)
[> s := x -> df(2)*(x-2)+f(2); (määrätään sivuajan yhtälö, kun x0=2)
[> plot ({f(x), s(x)}, x=-4..4);
Maplessa integraalifunktio ja määrätty integraali lasketaan samalla
komennolla int. Integraalifunktion laskeminen hoituu samalla tavoin
kuin derivointi. Esimerkiksi funktion f(x)=2x integraalifunktio voidaan
muodostaa näin: "int(2*x, x);". Jälkimmäinen suluissa olevista termeistä
on taas muuttuja, jonka suhteen integroidaan. Integraalifunktio voidaan
muodostaa kaikista jatkuvista funktioista, mutta monien funktioiden
integraalifunktiot ovat vaikeita löytää tai niiden ilmaiseminen
alkeisfunktioiden avulla on mahdotonta. Maple on hyödyllinen apuväline
hankalien integraalien tutkimiseen.
Integroidaan polynomifunktio f(x)=x^3-2x.
[> f := x -> x^3-2*x;
[> int (f(x), x);
Vastaukseksi saadaan (1/4)x^4-x^2. Maple ei oletusarvoisesti kirjoita
näkyviin integroimisvakiota. Mikäli integraalifunktiota käytetään johonkin
muuhun sovellukseen kuin määrätyn integraalin laskemiseen, on vakio
kuitenkin huomioitava. Differentiaaliyhtälöitä ratkaistessaan Maplekin
ottaa vakion mukaan.
Integroidaan 1/x.
[> int(1/x, x);
Maple antaa vastaukseksi ln x. On kuitenkin huomattava, että
integraalifunktio saa arvot myös, kun x<0. Täydellinen vastaus onkin ln
|x| + C, mitä Maple ei myöskään oletuksena näytä.
On iso joukko funktioita, joiden integraalit Maple joutuu ilmaisemaan ns.
erikoisfunktioiden avulla; näitä funktioita ei voi ilmaista tähän
mennessä tuntemiemme funktioiden avulla. Osan mahdollisista
integraalifunktioista Maple jättää kokonaan tai osittain ratkaisematta.
Tämä johtuu siitä, että joko integraalin ratkaiseminen on erittäin vaikeaa
ja/tai integraalifunktioita ei voi esittää missään sievemmässä muodossa.
Esimerkki funktiosta, jonka ratkaisussa Maple joutuu käyttämään
erikoisfunktioita on e^(x^2). (Kokeile!)
Piirretään kuvaaja integraalifunktioistakin: nyt piirrämme näkyviin
funktion f(x)=2 integraalifunktioineen.
[> f := x -> 2;
[> plot({f(x), int(f(x), x)}, x=-4..4);
On helppo nähdä, että integraalifunktio kuvaa alkuperäisen funktion ja
x-akselin väliin jäävän pinta-alan kertymää liikuttaessa oikealta
vasemmalle. Itse asiassa integraalifunktio, jonka vakio on 0 (kuten
tapauksemme), kuvaa ko. kertymää täsmälleen siten, että sitä oletetaan
olevan 0 kohdassa 0. Tästä vasemmalle kertyminen on negatiivista ja
oikealle positiivista.
Integroimme vielä funktion, jonka integroinnissa apuna voisi käyttää
sisäfunktion derivaattaa.
[> int(tan(x), x);
Tulokseksi saadaan -ln(cos(x)) (katso johto kurssin materiaalista).
Kosinin ympärillä pitäisi taas olla itseisarvomerkit, koska myös sen
negatiivisilla arvoilla integraali on määritelty. Sen sijaan kun cos(x) on
0, integraalifunktio ei ole sen paremmin määritelty kuin alkuperäinenkään
funktio.
Määrätty integraali lasketaan samoin kuin integraalifunktiokin, mutta
muuttujan tilalle integroimislausekkeeseen kirjoitetaan
"muuttuja=integroimisväli". Esim. sin(x):n integraali nollasta yhteen
saadaan kirjoittamalla
[> int(sin(x), x=0..1);
Tämä vastaus on jälleen symbolisessa muodossa. Numeerinen integrointi
tapahtuu tästä yksinkertaisesti evalf-komennolla.
[> evalf(int(sin(x), x=0..1));
Nyt saadaan kysytylle integraalille desimaalilikiarvo.
Huomaa, että käyrän ja x-akselin välisen alan selvittämisessä on ensin
otettava selville funktion nollakohdat (esim. solve-komennon avulla;
oletamme, että funktio on jatkuva) ja funktion merkki nollakohtien
välillä. Vasta sitten integroidaan kukin väli erikseen, otetaan
negatiivisista integraaleista vastaluvut, ja lasketaan kaikkien osavälien
antamat arvot yhteen! Esim. "int(sin(x), x=-1..1);" antaa tulokseksi 0,
koska välillä on yhtä paljon positiivisella ja negatiivisella puolella
x-akselia olevaa alaa. Käyrän ja akselin väliin jäävän alan saa selville
tässä tapauksessa näin:
[> -int(sin(x), x=-1..0)+int(sin(x), x=0..1);
Tai näin:
[> int(sin(x), x=0..-1)+int(sin(x), x=0..1);
(Takaperin integroiminen antaa saman tuloksen kuin etuperin
lukuunottamatta etumerkkiä! Tämän voi helposti päätellä analyysin
peruslauseesta.)
... Tai näin:
[> int(abs(sin(x)), x=-1..1);
Jolloin funktiosta otettiin ensin itseisarvo. Numeerinen arvo alalle
saadaan evalf-funktiolla.
Harjoitus 9. Derivoi derivaatan määritelmällä (limit-komentoa
käyttäen) ja ilman funktiot f(x)=ln(x), g(x)=x^3-2x^2+x ja h(x)=e^x.
Piirrä funktiot ja derivaatat Maplella. Mikä pitäisi oikeastaan olla
f'(x):n määrittelyjoukko (tämä ei välttämättä näy kuvassa oikein)?
Entä mitä huomaat h(x):stä? Päättele, mikä on h(x):n toinen
derivaatta. Entä kolmas ja n:s? Etsi funktioiden derivaattojen nollakohdat
ja laske funktioiden arvot niissä.
Harjoitus 10. Muodosta funktion f(x)=sqrt(2x) integraalifunktio ja
laske sellaisen pyörähdyskappaleen tilavuus, joka muodostuu, kun f(x):n
käyrä pyörähtää syvyyssuunnassa x-akselin ympäri ja sen piirtämän pinnan
sisään jääneestä kuviosta leikataan viipale x=3:sta x=6:een. (Vihje: tämä
tehdään integroimalla 3:sta 6:een kappaletta leikkaavan ympyrän alaa,
jonka kaava on πf(x)2.)
Harjoitus 11. Integroi funktio f(x)=2sin(2x) -π:stä π:hin.
Laske sitten sen kuvaajan ja x-akselin väliin jäävä ala samalla välillä.
Maplessa voi ratkaista differentiaaliyhtälöitä dsolve-komennolla.
Komentoa käytetään samalla tavoin kuin tavallista solveakin, ratkaistavana
on nyt vain funktio. Ratkaisemme aluksi differentiaaliyhtälön yy'=3x^2.
Tämä on separoituva differentiaaliyhtälö, jonka ratkaisu on
y=sqrt(2x^3+C), missä C on vakio.
[> dsolve (y(x)*diff(y(x), x)=3*x^2, y(x));
Huomaa, että koneelle on kirjoitettava jokainen funktio suluissa olevine
muuttujineen ja derivaatat derivoimiskomennon avulla. Maple ei tunnista
merkintää y'.
Maple sieventää vastausta siten, että ilmoitettu ratkaisussa
esiintyvä vakio ei ole välttämättä integroimisvaiheessa saatu
integroimisvakio, vaan jokin siitä ratkaistessa syntynyt toinen vakio
(kuten tehdään myös oppimateriaalin kinkkutehtävässä: e^C on uusi vakio,
koska e ja C ovat molemmat joitain vakioita). Tällä ei ole merkitystä,
sillä vakio on kuitenkin vapaavalintainen, ellei alkuarvoehtoa ole
annettu.
Voimme yrittää ratkaista Maplella kuinka vaikeita differentiaaliyhtälöitä
tahansa. Käytännössä lineaarisia monimutakaisemmat differentiaaliyhtälöt
eivät usein ratkea Maplenkaan voimin. Kokeile esim. yhtälön
y''y'=sqrt(y)x ratkaisemista... Sen sijaan alkuarvotehtävien
ratkaiseminen Maplella käy helposti. Ratkaisemme alkuarvotehtävän y'=y,
y(0)=1 (tämä on materiaalissakin esiintyvä e^x:n määritelmä).
[> dsolve ({diff(y(x), x)=y(x), y(0)=1}, y(x));
Koneen pitäisi antaa vastaukseksi y(x)=ex. Tämä on ainoa
funktio, joka on itse oma n:s derivaattansa mielivaltaisella n. Yhtälö ja
alkuarvo ryhmitellään dsolve-komennossa siis omaksi ryhmäkseen
aaltosulkeiden sisään, kuten yo. kaavassa on tehty.
Toinen esimerkki alkuarvotehtävästä on materiaalin "kinkkutehtävä". Siinä
lämpötilaa T kuvaa differentiaaliyhtälö T'=k(200-T), missä T on t:n eli
ajan funktio ja k tuntematon vakiokerroin (tässä verrannollisuuskerroin).
Alkuarvoehto oli tässä tapauksessa T(0)=21.
[> dsolve ({diff(T(t), t)=k*(200-T(t)), T(0)=21}, T(t));
Tämä ratkaisee kinkun lämpötilaa kuvaavan funktion lukuunottamatta k:n
arvoa, jota ei näillä ehdoilla voidakaan saada selville. Huomaa, että
ratkaisussa kerroin e^C on muutettu pelkäksi vakioksi edellä kuvatulla
tavalla.
Harjoitus 12. Ratkaise differentiaaliyhtälö y'=(x+2)/(2y-1) käsin
ja koneella. Ratkaise se sitten alkuarvolla y(0)=3 käsin ja koneella.
Harjoitus 13. Ns. Mooren lain mukaan tietokoneiden
laskentakapasiteetin kasvu on suoraan verrannollinen kulloisenkin
ajanhetken laskentakapasiteettiin. Ratkaise kulloistenkin tietokoneiden
maksimikapasiteettia kuvaava indeksiluku i(t) ajan funktiona, kun
maksimikapasiteettia kuvaava indeksiluku oli vuonna 2000 i(t)=100 ja
vuonna 2002 i(t)=200. (Vinkki: käytä ensimmäistä alkuarvoa
dsolve-komennossa integroimisvakion ratkaisemiseen ja toista sen jälkeen
verrannollisuuskertoimeen.)
Toinen tehtävä: puolitusmenetelmä
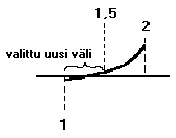




Kolmas tehtävä: Newtonin menetelmä



Neljäs tehtävä: Numeerinen integrointi

Viides tehtävä: Tilastolliset tunnusluvut ja regressio
Kuudes tehtävä: Matriisinkäsittelyä Excelillä

Tällöin tuloksen pitäisi ilmestyä maalatulle alueelle.
| 3 -4 2 | | 1 0 -2 |
A = | -1 0 1 | ja B = | -3 -4 -3 | .
| 2 1 -3 | | 2 -5 2 |
Laske matriisit A+B ja AB. Laske lisäksi matriisit ABAB, ABABAB, ... ,
ABABABABABABABABABABABAB.
16a + 8b + 4c + 2d + e = -10
81a - 27b + 9c - 3d + e = -135
a - b + c - d + e = 5
16a - 8b + 4c - 2d + e = -18
256a - 64b + 16c - 4d + e = -450
käänteismatriisin avulla luentomateriaalissa esitetyllä tavalla.
Maple-osio
1. Laskemista Maplella
0
-1
2. Lausekkeita ja kuvaajien piirtäminen
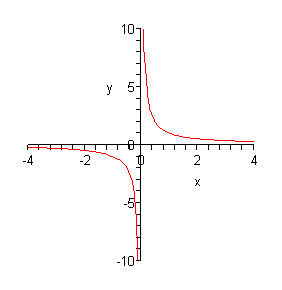
3. Funktioita ja niiden kuvaajia
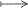 ). Maplessa nuolen alkuun tulee siis
muuttuja ja loppuun
riippuvuusehto. Määrittelemme nyt funktion f(x)=x^3-2x.
). Maplessa nuolen alkuun tulee siis
muuttuja ja loppuun
riippuvuusehto. Määrittelemme nyt funktion f(x)=x^3-2x.
[> f(3);
21
[> f(Pi*I);
3
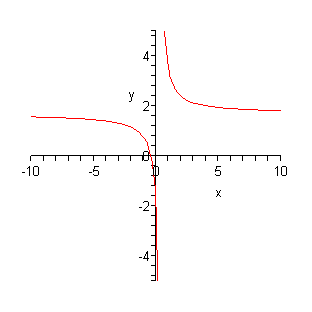
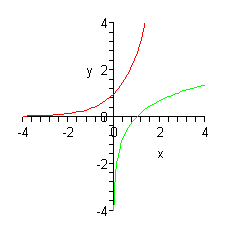
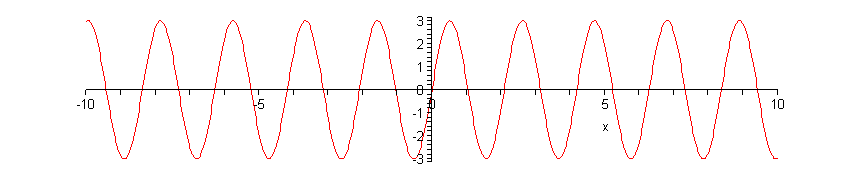
4. Raja-arvo
5. Derivaatta ja integraali
Derivointi
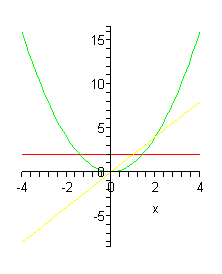
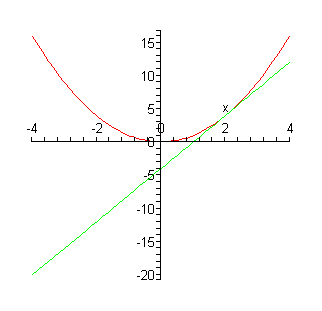
Integrointi
6. Differentiaaliyhtälöiden ratkaiseminen