¹¹ In this footnote, I propose a formal definition of threat. Denote by X_π(s) the random variable giving the total discounted future reward starting from initial state s, following policy π, and using discount factor λ. That is, X_π(s) = ∑ _t=0^∞λ^tr _t | π,s(0) = s. The expectation of this quantity is nothing else than the state-value function, and that will be used as the baseline. Thus, subtracting the baseline we obtain the random variable 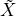_π(s) = X_π(s) - V _π(s) = ∑ _t=0^∞λ^t(r _t - E{r_t}) | π,s(0) = s. 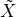Some measure of the downside risk (negative tail) of _π(s) is now defined a measure of threat for state s. We could use, for example, the conditional value-at-risk (expected shortfall), see footnote 7 in this chapter for discussion of various downside risk measures.