Viewing Transformation is the mapping of coordinates of points and lines that form the picture into appropriate coordinates on the display device.

  World coordinate system (WCS) is the right handed cartesian co-ordinate system where we define the picture to be displayed.   A finite region in the WCS is called the Window. The corresponding coordinate system on the display device where the image of the picture is displayed is called the physical coordinate system. Mapping the window onto a subregion of the display device called the viewport is called the Viewing Transformation. Normalized device coordinate (NDC) is the display area of the virtual display device corresponding to a unit square. The lower left handed corner is the origin of the coordinate system. Mapping the window in the world coordinate space to viewport in NDC space is called the Normalization Transformation, N.

where is the scale in x and y directions, given by

View Transformation

A 3D scene can be viewed from any posistion in 3D space. A "synthetic" camera positioned and oriented in 3D space can be used to describe the viewing, and the part of the image or scene to be viewed . It has the following three principal ingredients.

1. View plane: The window is defined in this plane.
   • The origin of this plane which defines the position of the eye or camera is called the view reference point .
   • A unit vector to this plane is the view plane normal .
   • Another vector called the viewup vector is a unit vector perpendicular to .
2. View coordinate system: Usually a left handed system called the UVN system is used.
   • , the y-axis of the view coordinate system is the perpendicular projection of on the view plane.
   • , the x-axis of the view coordinates, is orthogonal to and i.e.

     

   • Positive and are to the right and up-direction from eye's point of view.
   • is the z-axis of the view coordinate. It increases in positive direction with depth of a point from the eye.
3. An eye defined within this system. and e determines a plane orthogonal to containing e.

Let be the look-at-point. For perspective views, the view plane normal as a unit vector from eye to a ``look-at point'' is given by

The view up vector is the tilt (rotation) of the head or camera.

For parallel views it is convenient to think of the view plane normal as determining the direction of projection.

View Coordinate System

An object in world coordinate space, whose vertices are can be expressed in term of view coordinates .

• Translate the view reference point e to the origin
• Rotate about world coordinate y axis to bring the view coordinate axis into the yz plane of world coordinates
• Rotate about the world coordinate x axis until the z axes of both systems are aligned
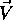• Rotate about the world coordinate z axis to align the axis with the y
• Reflect relative to the xy plane, reversing sign of each z coordinate to change into a left-handed coordinate system

Example of View Transformation

• Let be the view reference point.
• Let be the look-at point.
• Let be the up vector.
  • Translate:

    

  • Rotate about y:

    

  • Rotate about x:

    

  • Rotate about z: Identity
  • Reflection:

    

  • Composite transform V: