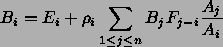
Radiositeettimenetelmä

Lämpösäteilyn mallintamiseen käytettyä radiositeettimentelmää on sovellettu myös tietokonegrafiikkaan. Menetelmässä lasketaan valonlähteistä tulevan energian jakautuminen ympäristöön, olettaen ideaalisen diffuusin heijastuksen pätevän ympäristön pinnoille. Tämän jälkeen voidaan käyttää jotain perinteistä kuvanmuodostumenetelmää, ja intensiteetti interpoloivaa valaistusta lopullisen kuvan tekemiseen. Saatu tulos ei riipu katselijan paikasta ympäristössä.

Radiositeettiyhtälö on n:lle pintalapulle

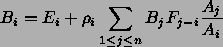
Bi on pintalapun i radiositeetti (säteilevä JA heijastuva energia / aika-yksikkö / pinta-ala yksikkö)
Ei on pintalapun säteilemä energia (valonlähteet)
Fij on näkyvyys- tai muotokerroin, eli kertoo kuinka suuri osa pintalapusta i lähtevästä energiasta päätyy pintalapulle j. Tämä on ainoastaan geometrian funktio.
Ai on pintalapun i pinta-ala.
ri on pintalapun heijastuvuus (aallonpituuden funktio)

Nyt pätee

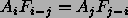
jolloin ensimmäinen yhtälö voidaan kirjoitaa yksinkertaisemmin

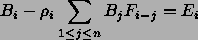
Tämä on nxn lineaarinen yhtälöryhmä josta pintalappujen radiositeetit voidaan ratkaista. Matriisi on suuri, täysi ja diagonaalidominantti, eli iteraatiomenetelmät yhtälön ratkaisemiseksi ovat paikallaan.

Esimerkki radiositeettimenetelmällä lasketusta kuvasta ja laskentaverkko.

Muotokertoimet

Muotokerroin differentiaaliselta alueelta dAi differentiaaliselle alueelle dAj on

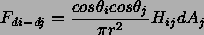
josta integroimalla pinta-alojen yli saadaan muotokerroin pintalapulta Ai pintalapulle Aj

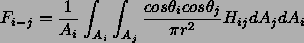
Kulmat yhtälöissä ovat pintalappujen normaalien ja pintojen pisteiden välisen suuntavektorin välisiä. Hij on termi pintojen välissä olevien esteiden huomioon ottamiseksi, joka voidaan evaluoida vaikkapa säteenheittoalgoritmilla.

Piirtovaiheessa intensiteetit tarvitaan yleensä pintalappujen kulmapisteissä (intensiteetti-interpolointi valaistus). Tämä voidaan tehdä paitsi keskiarvoistamalla yhteen verteksiin liittyvien pintalappujen intensiteetit laskennan päätyttyä, myös laskemalla radiositeettiyhtälö suoraan kulmapisteille, jolloin muotokerroin saadaan integroimalla vain toisen alueista yli.

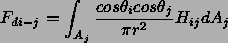
Toisen pintalapun radiositeetti voidaan ottaa esimerkiksi keskiarvona kulmapisteiden radiositeeteista.