in the line 
to
produce the point 
:
The chosen transformation is one which has superficially very little
relationship to translation, scaling or rotation. It is the reflection
of a point in the line to
produce the point :
The steps followed in building the composite transformation are always in a fixed sequence. The first thing to do is to translate everything so that the line intersects the origin of the new co-ordinate system.
The appropriate translation matrix is also shown. Note that that the
transformed point is also moved by this
translation.
The next thing to do is to rotate the line so that it lies along either the x or y axes. It doesn't matter which one is chosen, so I have decided arbitrarily to rotate the line by -45 degrees so that it lies along the x axis.
Again, note that everything is transformed by this rotation, including
the point .
Now that the line lies along either the x or y axis, it is trivial to perform the reflection by using a scaling transformation.
In this case we are reflecting in x so y changes sign but x is unaffected.
Finally we have to get back to the original co-ordinate system, which requires us to invert the original rotation:
and finally to invert the original translation:
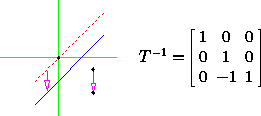
This gives an expression in terms of matrix multiplication for the composite transformation:
Here is the process of multiplying out the matrices to generate M:
Here is the result of multiplying a homogeneous source point by the composite matrix:
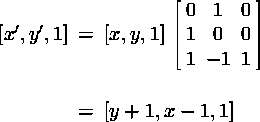
The point about this process is not that it is the simplest or quickest way to generate the required transformation for a human, but that is is a rigorous sequence of steps suitable for a machine. Thus, when designing a computer graphics system we normally endow it with the smallest possible set of primitive transformations and let more complex ones be built up in the manner shown.
Note that it doesn't matter how complex the sequence of primitive transformations needed to generate the composite matrix M because this is only done once. When transforming points we multiply them by M alone, so it doesn't matter how difficult it is to set M up.
A further point worth noting is that rotations, translations and scaling operations (and their compositions) always map straight line segments in the object co-ordinate system to straight line segments in the world co-ordinate system. This means that multiplication by M need only be performed on the end points of straight line segments, and not on every intermediate point.
This property is only true of straight line segments, not of other curves in general. Thus, a general affine transformation applied to a circle converts it into an ellipse, etc. Transforming such curves requires either that they be represented as a set of line segments or that every point (at screen resolution) be individually transformed.
The ease, and low cost, with which straight line segments may be transformed accounts for their popularity as primitive elements for modelling scenes in computer graphics.
From Colin Flanagan -- see details
26.11.1996