Exercise session 5

Introduction to bioinformatics, Autumn 2008

Exercise sessions:

Tuesday 7 October 16.15-18.00 Exactum C221
Wednesday 8 October 14.15-16.00 Exactum B120

Remember to send your exercise notes to Lauri Eronen before your exercise session begins!

Note: these are the last exercises on the course!

Assignments

Find the total parsimony cost with the algorithm given in lectures for the tree

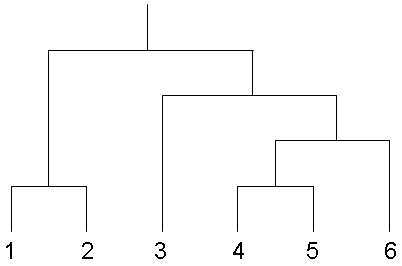
given the following set of sequences
```
        1 ATAG
        2 AGAG
        3 CAAG
        4 CGCG
        5 CGAG
        6 CGTA
      
```
Indicate F and L at each node of the tree.
1. Find an unrooted phylogenetic tree corresponding to the distances in the following matrix D.
  
  a b c d e
  
  a 0 9 3 10 8
  
  b 9 0 8 9 5
  
  c 3 8 0 9 7
  
  d 10 9 9 0 8
  
  e 8 5 7 8 0
  
  Hint: consider additivity and assume that edges can be given integer weights.
2. Is the data in D ultrametric? Why or why not?
[exercise 3 from Deonier et al. p.287] Plot the scaled data for H. habilis, A. robustus, A. boisei, A. africanus, A. afarensis, and P. troglodytes presented in Section 10.5., p. 282 (data). Use a ruler to measure distances and sketch what you think the hierarchical relationships would be from hierarchical clustering by single linkage. Does the situation change if complete linkage is applied?
Use K-means to cluster the data in exercise 3, where k=2. Select two arbitrary initializations and plot the trajectory how the cluster centroids move with each iteration.
Computer exercise: Perform hierarchical clustering using the programming language R on the dataset named toydata.txt. Try out different clustering criteria, and plot each of the results. How many clusters would you say there is in the data?

Useful R commands (try writing e.g. ?dist in the R promt to get help; help.start() might be useful as well):
```
      read.table
      dist
      hclust
      plot
      
```

Computer exercise: Perform k-means clustering on the data above. Compute the sum of within sum of squares for increasing number of centroids k. What is the optimal number according to the heuristic of Deonier et al, p. 285? Project the data to two principal components and plot the data. Can you see clusters in there?

Useful R commands:

        kmeans
        - The object returned by kmeans has a field withinss, you can access that by [object name]$withinss
        prcomp
        - The object returned by prcomp has a field rotation which contains the principal components.
        Projection: matrix multiplication (%*%) of first two principal components and the data.
        transpose of a matrix M: t(M)